Standard and Scientific Notation
- Understanding Scientific Notation and Standard Notation
- Scientific Notation – Real-World Application
- Converting from Standard to Scientific Notation – Steps
- Converting from Scientific to Standard Notation – Steps
- Converting from Scientific to Standard Notation – Examples
Learning text on the topic Standard and Scientific Notation
Understanding Scientific Notation and Standard Notation
Welcome to the intriguing world of Scientific Notation. This mathematical concept is a game-changer when dealing with super large numbers like the number of stars in the universe or really tiny ones like the size of molecules in chemistry. It’s a helpful tool that makes working with these extreme numbers much simpler. It is also known as standard form. Ready to learn how scientific notation makes big and small numbers a breeze to handle? Let’s get started!
Scientific Notation is a way of expressing large or small numbers as a product of a number between 1 and 10 and a power of ten. Standard Notation is our regular way of writing numbers. It is important to know the difference in these key words as sometimes scientific notation is also called standard form which can easily confuse the two representation types of numbers!
Scientific Notation – Real-World Application
Here's a table with real-world examples, illustrating their sizes in both standard and scientific notation:
| Item | Standard Form | Scientific Notation |
|---|---|---|
| Distance from Earth to Sun | 149,600,000 km | 1.496 × 108 km |
| Size of a Red Blood Cell | 0.000007 m | 7 × 10-6 m |
The first row represents the vast distance from the Earth to the Sun, while the second row shows the minuscule size of a red blood cell, each expressed in a form that best suits their scale.
Converting from Standard to Scientific Notation – Steps
Converting numbers from standard to scientific notation can be done by following these steps:
| Step | Direction | Example |
|---|---|---|
| 1 | Move the decimal point to get a number between 1 and 10, with only one non-zero digit to its left. | For 12,345, move the decimal between the 1 and 2. 1.2345 |
| 2 | Count how many places you moved the decimal. | Decimal moved 4 places to the left. |
| 3 | Write the exponent based on your count. Positive for left moves (large numbers), negative for right (small numbers). | 12,345 in scientific notation is 1.2345 × 104 |
When working with conversions from standard form, you may be asked to convert an expression to an ordinary number. You can try this in the practice problems that follow this set.
Converting from Scientific to Standard Notation – Steps
Converting numbers from scientific to standard notation is the reverse process, with the following steps.
| Step | Direction | Example |
|---|---|---|
| 1 | Start with the number in scientific notation. | For 3 × 104, start with 3 |
| 2 | Move the decimal point based on the exponent. Right for positive exponents, left for negative. | Move decimal 4 places to the right. |
| 3 | Fill in with zeros if needed, to match the number of places you moved the decimal. | 3 becomes 30,000 (standard notation/ordinary number) |
Check your understanding of these two conversions.
Converting from Scientific to Standard Notation – Examples
Standard and Scientific Notation – Exercises
Standard and Scientific Notation – Summary
Key Points from This Text:
- Standard notation is the regular form of a number we typically see in the world. For example: 50,800,000.
- Scientific notation makes it easier to work with very large or small numbers.
- Numbers in scientific notation are also referred to as being in standard form so it is important to know the key terminology.
- Scientific notation is written as a product of a decimal between 1 and 10, and a power of ten, for example: 5.08 × 107.
- The exponent shows how many times the decimal moves, with positive for large and negative for small numbers.
| Conversion Type | Process |
|---|---|
| Standard to Scientific Notation | Move decimal to get a number between 1-10, count moves, times 10 to the power of moves. |
| Scientific to Standard Notation | Start with scientific notation number, move decimal based on exponent (right for positive, left for negative). |
For more practice with this topic, this video is helpful for learning how to compare numbers written in scientific notation - Choosing Appropriate Units with Scientific Notation
For more exciting maths topics, explore our interactive problems, videos and worksheets on our website!
Standard and Scientific Notation – Frequently Asked Questions
Standard and Scientific Notation exercise
-
Convert an ordinary number into standard form.
HintsTo convert from an ordinary number to standard form:
- Rewrite the number as a number between $1$ and $10$
- Count how many jumps it would be to get the number as it was
- The power of $10$ is the number of jumps needed.
If we write a number between $1$ and $10$ we have to multiply by $10$ a number of times to get it back to its original number.
For example, $2,000$ can be written as $2$ but it is not equal unless we multiply by $1,000$.
We write $2,000 = 2\times1,000 = 2\times10^{3}$
Solution- $400 = 4\times10^{2}$
- $4,000 = 4\times10^{3}$
- $450 = 4.5\times10^{2}$
- $4,500 = 4.5\times10^{3}$
- $45,000 = 4.5\times10^{4}$
- $405 = 4.05\times10^{2}$
-
Convert an ordinary number into standard form.
Hints- Place the decimal point after the first non-zero digit
- Count the places moved from the decimal’s original location
If we have a very small number and write it as a number between $1$ and $10$, then the powers will be negative in order to make it very small again.
SolutionThe correct answer is $6.3\times10^{-4}$
- Place the decimal point after the first non-zero digit $6.3$
- Count the places moved from the decimal’s original location $-4$
-
Convert the standard form into ordinary numbers.
Hints$1.7\times10^{2}$ means the number is multiplied by $100$.
The number moves $2$ places to the left.
$1.7\times10^{-2}$ means the number is divided by $100$.
The number moves $2$ places to the right.
Solution- $5.8\times10^{2} = 580$
- $5.8\times10^{3} = 5,800$
- $5.8\times10^{-2} = 0.058$
- $5.8\times10^{-1} = 0.58$
-
Find the ordinary number.
HintsMultiplying by $10^{6}$ means multiply by $10$ six times.
Moving the number to the left.
Check out the example pattern to help you.
- $3.21\times10^{1} = 32.1$
- $3.21\times10^{2} = 321$
- $3.21\times10^{3} = 3,210$
Solution$9.43\times10^{6} = 9,430.000$
We multiply $9.43$ by $10$ six times.
Move the number to the left, six places making it bigger.
-
Find the powers of ten.
Hints- $10 = 10\times1 = 10$
- $100 = 10\times10 = 10^{2}$
The power is the number of times we multiply by $10$.
For example , if we multiply a number by $10$ six times, we can write it as $10^{6}$
Solution- $100 = 10^{2}$
- $1,000 = 10^{3}$
- $10,000 = 10^{4}$
- $100,000 = 10^{5}$
$1,000 = 10\times10\times10$
We can write it as $10^{3}$
-
Mixed standard form and ordinary numbers
Hints- Change the two ordinary numbers into standard form to make them easier to compare
- We place the decimal point after the first non-zero digit
- Count the jumps back to the original location.
Write all the standard form numbers underneath each other to help compare.
For example,
Solution- $1.2\times10^{-5}$
- $0.00019$
- $1.1\times10^{-3}$
- $1.8\times10^{-3}$
- $0.0099$

Rational Numbers on the Number Line
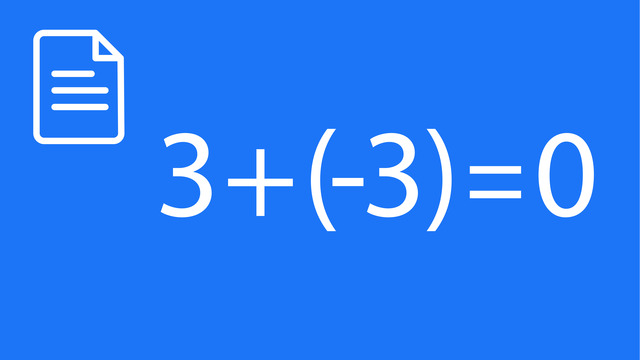
Subtracting Integers

Solving Problems with Negative Numbers
Multiplying and Dividing Integers

Rational and Irrational Numbers
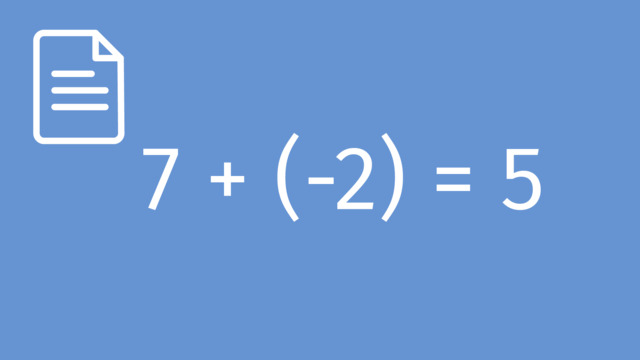
Subtracting Rational Numbers by adding the Inverse

Analysing Numerical Patterns
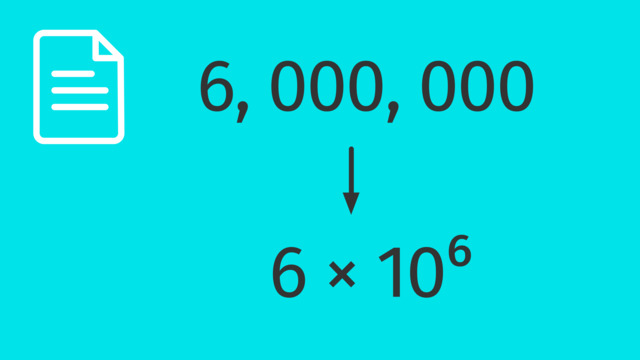
Standard and Scientific Notation
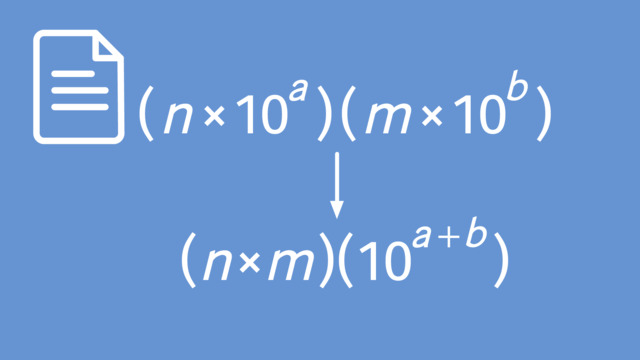
Using Operations with Scientific Notations
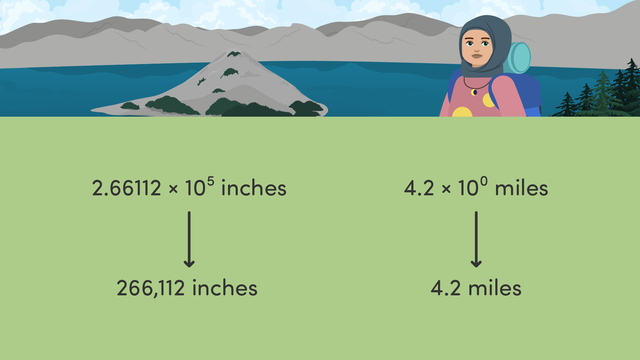
Interpreting Scientific Notation
 Do you want to learn faster and more easily?
Do you want to learn faster and more easily?













