Multiplying and Dividing Integers
- Multiplying and Dividing Integers
- Understanding the Rules of Multiplication and Division
- Multiplying Integers
- Dividing Integers
Learning text on the topic Multiplying and Dividing Integers
Multiplying and Dividing Integers
In mathematics, multiplying and dividing integers involves working with both positive and negative numbers. These operations are essential in various real-life scenarios, such as accounting, temperature changes, and sports statistics. Integers are whole numbers so we will focus on these but the same concepts apply to fractions and decimals once you have mastered the concepts we will look at here.
Multiplying integers is the process of combining two or more integers to find their product. Dividing integers, on the other hand, is the process of splitting a quantity into equal parts.
Understanding the Rules of Multiplication and Division
To master multiplication and division with integers, it's crucial to know the basic rules. These rules tell us what happens when we multiply or divide positive and negative numbers. They're like guiding principles that help us figure out the results of maths problems involving integers. Once we understand these rules, we can solve different kinds of problems more easily. Another word for multiplication is product and an alternative word for dividing is quotient.
Multiplying Integers
| Rule | Outcome |
|---|---|
| Product of two positive integers | Positive |
| Product of two negative integers | Positive |
| Product of a positive and a negative integer | Negative |
Take a look at some examples:
- $3 \times 4 = 12$
- $(-2) \times (-5) = 10$
- $6 \times (-2) = -12$
- $(-3) \times 2 = -6$
- $8 \times 0 = 0$ (It is important to know zero is neither negative nor positive! It is known as a neutral integer.)
Dividing Integers
| Rule | Outcome |
|---|---|
| Quotient of two positive integers | Positive |
| Quotient of two negative integers | Positive |
| Quotient of a positive integer and a negative integer | Negative |
Take a look at some examples:
- $12 \div 3 = 4$
- $(-10) \div (-2) = 5$
- $15 \div (-3) = -5$
- $\frac{-18}{3} = -6$
- $\frac{-24}{-4} = 6$
Multiplying and Dividing Integers – Practice
Practice applying these rules here!
Multiplying and Dividing Integers – Summary
Key Learnings from this Text:
- Understanding the rules of multiplying and dividing integers is crucial for solving mathematical problems involving positive and negative numbers.
- Multiplication results in a positive product when both integers have the same sign, while different signs yield a negative product.
- Division follows a similar pattern, with the quotient being positive for like signs and negative for unlike signs.
- Mastery of these rules enables efficient problem-solving in real-life applications such as accounting, temperature conversions, and sports statistics.
- Practice exercises provided in the text reinforce comprehension and application of these multiplication and division rules.
Once you have mastered the rules of multiplying and dividing integers, you can also learn the art of subtracting integers, and of course adding integers.
Multiplying and Dividing Integers – Frequently Asked Questions
Multiplying and Dividing Integers exercise
-
Multiply the positive and negatives.
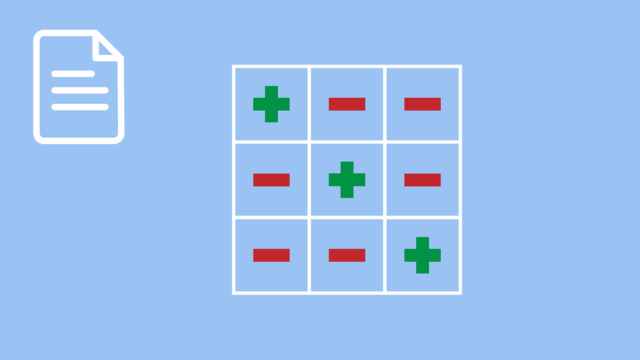
HintsEach equation which has a product has two negatives and one positive, unless it is three positives. See the rows in the diagram.
- If we have $(-) \times (-)$ then the answer is $(+)$, two negatives and one positive.
- If we have $(+) \times (-)$ then the answer is $(-)$, two negatives and one positive.
- If both signs are the same the answer is $(+)$.
- If both signs are different, the answer is $(-)$
There are $4$ correct answers!
SolutionCorrect answers are:
- $(+) \times (-) = -$
- $(-) \times (+) = -$
- $(-) \times (-)= +$
- $(+) \times (+) = +$
-
Multiply the integers.
HintsWith a product, there are two negatives and one positive.
For example, $(-) \times (-) = +$ or $(-) \times (+) = -$.
- Same signs $= (+)$ answer, $5 \times 5 = 25$ and $-5 \times -5 = 25$.
- Different signs $= (-)$ answer, $-5 \times 5 = -25$ and $5 \times -5 = -25$
Solution- Same signs $= (+)$ answer.
- Different signs $= (-)$ answer.
-
Find the questions.
HintsMultiplication and division with negative integers are done the same way.
- $(- \times + = -)$ or $(- \div + = -)$
- $(- \times - = +)$ or $(- \div - = +)$
- $(+ \times - = -)$ or $(+ \div - = -)$
- $(+ \times + = +)$ or $(+ \div + = +)$
To have an answer of a negative, the question must have one negative and one positive integer. For example,
- $80 \div -10 = -8$.
- $-80 \div 10 = -8$.
- $8 \times -10 = -80$.
- $-8 \times 10 = -80$.
There are $3$ correct answers here.
SolutionCorrect answers are:
- $-4 \times 2 = -8$
- $16 \div -2 = -8$
- $1 \times -8 = -8$
-
Find the missing integers to make the calculation correct.
HintsMultiplication and division are the inverse of each other.
$4 \times 5 = 20$ is equal to $20 \div 5 = 4$, and $20 \div 4 = 5$
If $10 \times ? = -20$ , we can rewrite it as $-20 \div 10 = -2$. Therefore, the missing integer is $-2$.
- If the signs are the same the answer is positive.
- $(-) \times (-) = +$ and $(-) \div (-) = +$
- If the signs are different, the answer is negative.
- $(-) \times (+) = -$ and $(+) \div (-) = -$.
Solution- $-3 \times ? = -15$ is the same as $-15 \div -3 = 5$
- $-3 \div ? = 5$ is the same as $15 \div 5 = 3$
- $? \times -5 = 15$ is the same as $15 \div -5 = 3$
- $-15 \div ? = 3$ is the same as $-15 \div 3 = -5$
-
Divide the integers.
HintsDividing integers works the same way as multiplying. See the diagram and apply it to a division.
- If we have $(-) \div (-)$, then we must use a $+$ for the answer.
- If we have $(-) \div (+)$, then we must use a $-$ for the answer.
SolutionThe correct answer is $20 \div -4 = -5$.
- We divide the absolute values first.
- $20 \div 4 = 5$
- When we use the rule, signs are different so answer is positive.
- That is $(+) \div (-) = -$.
- Answer is therefore, $-5$.
-
Multiply or divide the integers.
HintsTo work out the next terms, we must first work out what the term is multiplied by to get to the next. We call this the common ratio.
For example, $4, -20, ....$ we do $-20 \div 4 = -5$. That means each term is multiplied by $-5$ to get the next term.
To find the common ratio (the multiplier) we do,
$2 \times ? = -6$ or $-6 \div 2 = ?$
SolutionThe correct answer is $-54$ and $162$.
- To find the common ratio, we do $2 \times ? = -6$
- Which is the same as $-6 \div 2 = -3$
- $-3$ is the multiplier, so to get the next term we multiply by $-3$
- $-6 \times -3 = 18$
- $18 \times -3 = -54$
- $-54 \times -3 = 162$

Rational Numbers on the Number Line
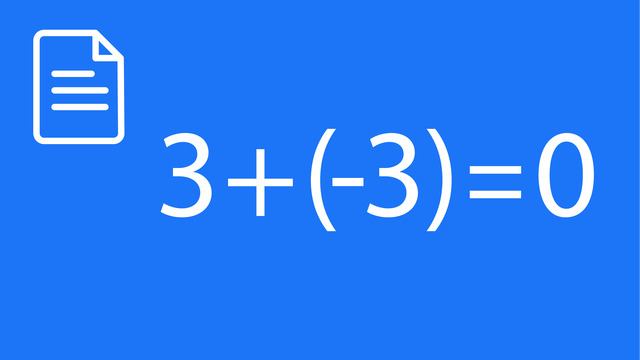
Subtracting Integers

Solving Problems with Negative Numbers
Multiplying and Dividing Integers

Rational and Irrational Numbers
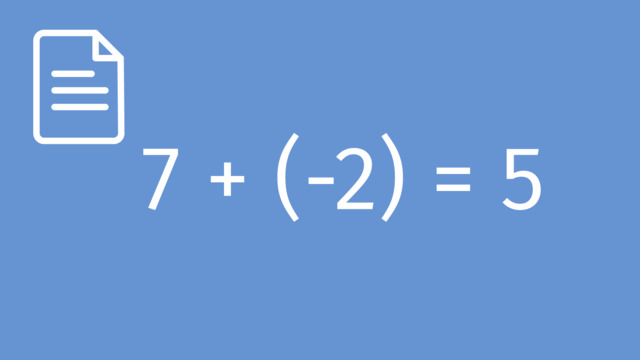
Subtracting Rational Numbers by adding the Inverse

Analysing Numerical Patterns
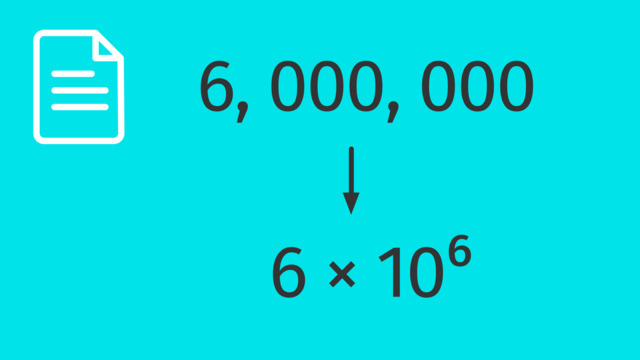
Standard and Scientific Notation
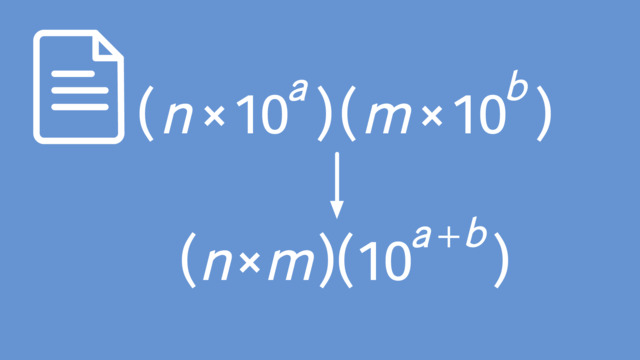
Using Operations with Scientific Notations
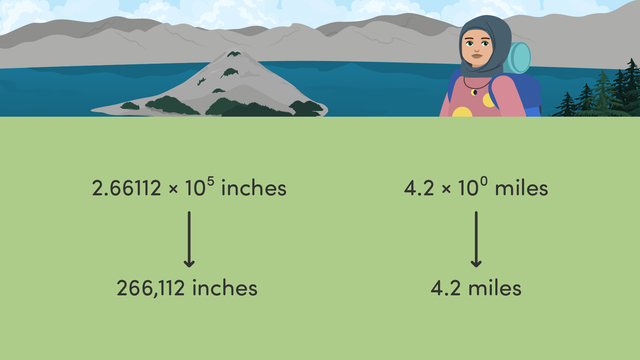
Interpreting Scientific Notation
 Do you want to learn faster and more easily?
Do you want to learn faster and more easily?











