Solving Problems with Negative Numbers
- What Are Negative Numbers?
- Understanding Negative Numbers
- Interpreting Negative Numbers in Calculations
- Negative Numbers – Problems in Various Contexts
- Temperature Below Freezing
- Bank Overdraft
- Elevation Below Sea Level
Learning text on the topic Solving Problems with Negative Numbers
What Are Negative Numbers?
In this text, we will explore the concept of negative numbers. Understanding negative numbers is important in mathematics and everyday life. We will learn how to work with negative numbers, perform operations, and solve problems involving negative values. Let's dive in!
Understanding Negative Numbers
Negative numbers are numbers less than zero. They are represented with a minus sign (-) in front of them.
Negative numbers are used in various contexts, such as temperatures below freezing, floors below ground level in buildings, bank accounts or depths below sea level. Therefore, understanding, being able to interpret and solve problems with negative numbers is extremely important.
Interpreting Negative Numbers in Calculations
To interpret negative numbers in different contexts, we need to understand that they represent numbers below zero. Bringing these numbers to life, and applying them to temperatures, makes things easier to understand. For example, -5°C means it is 5 degrees below freezing. Counting forward and backwards with positive whole numbers helps us understand temperature changes.
For instance, if the temperature increases by 3 degrees, or in other words it gets three degrees warmer, we count forwards from the initial temperature by adding 3. If the temperature decreases by 2 degrees, or it gets 2 degrees colder, we count backwards from the initial temperature by subtracting 2.
In order to solve problems with negative numbers, follow these simple steps:
| Step | What to do |
|---|---|
| 1. | Identify the initial number |
| 2. | Decide if you need to count forwards or backwards |
| 3. | Complete the calculation |
| 4. | Find the result |
Negative Numbers – Problems in Various Contexts
To deepen our understanding of negative numbers, let's explore more examples that illustrate how they work in various contexts.
Temperature Below Freezing
If the temperature drops to -5°C at night and rises by 10°C during the day, what is the daytime temperature?
Bank Overdraft
If Sam's bank account balance is -£50 (which means he is in overdraft), and he deposits £100, what is his new balance?
Elevation Below Sea Level
The Dead Sea has an elevation of -423 metres below sea level. If a diver descends another 10 metres, what is the diver's new elevation?
Negative Numbers – Additional Exercises
Practising with negative numbers helps solidify the concept. Here are some additional exercises to try.
Negative Numbers – Summary
Key Learnings from this Text:
- Negative numbers are numbers less than zero and are represented with a minus sign (-).
- Negative numbers are used to represent values below a reference point or in the opposite direction.
- Negative numbers are often seen in word problems about temperatures, height below sea level and money.
- Adding a negative number to a positive number results in a smaller value, while subtracting a negative number results in a larger value.
Remember to practise working with negative numbers to strengthen your understanding. If you want to explore more maths topics, check out our website for interactive practice problems, videos and printable worksheets. Keep up the great work!
Negative Numbers – Frequently Asked Questions
Solving Problems with Negative Numbers exercise
-
Can you complete the number line?
HintsRemember, negative numbers have a minus sign ($-$) in front of them and are less than zero.
Use the numbers already filled in to help you.
$-7$ is less than $-6$ so it will come before $-6$ on the number line.
SolutionHere we can see the completed number line.
-
Where is Lucy?
HintsLucy is currently on floor 2 and she is travelling down so the number of the floor will be less than than 2.
We need to solve 2 - 4 to find the new floor.
Count down four times from 2 to find the new floor.
SolutionLucy is now on - 2.
Lucy started on floor 2 and travelled four floors down so we needed to solve 2 - 4. We can see on the number line above if we jump four times backwards from 2, we get to - 2.
-
How much money is in Bill's bank account?
HintsTo solve this problem we start at $-12$. What are we adding to $-12$?
We need to solve $-12 + 15$.
The answer is a positive number.
SolutionBill is in his overdraft and currently has $-£12$ in his bank account. For his birthday, his Grandma gave him $£15$. Now Bill has $\textbf£\textbf3$ in his bank account.
$-12 + 15 = 3$
-
What is the temperature?
HintsIf the temperature is warmer, we need to add or count forwards.
If the temperature is colder we need to subtract or count backwards.
We know that Tuesday is $5$ degrees warmer than Monday so we need to add $5$ to $-3$.
$-3$ + $5$ =
Use the number line to help you count forwards from $-3$.
SolutionMonday: $-3$ °C
Tuesday: $2$ °C
Wednesday: $-1$ °C
Thursday: $6$ °C
Friday: $8$ °C
Saturday: $2$ °C
Sunday: $0$ °C
__________________________________________
- Tuesday: $-3$ + $5$ = $2$
- Wednesday: $2$ - $3$ = $-1$
- Friday: $2$ + $6$ = $8$
- Sunday: $-1$ + $1$ = $0$
-
What do you know about negative numbers?
HintsHere are some negative numbers:
- $-4$
- $-7$
- $-110$
- $-20,341$
On this number line we can see the negative numbers to the left of zero which means they are smaller than zero.
There are two correct answers.
SolutionThe true statements are:
- Negative numbers are less than zero.
- Negative numbers are represented with a minus symbol (-) in front of them.
-
Can you solve the problems?
HintsTo find the level Axel and Tank are now at, add $43$ to $35$.
To find the average temperature in summer, add $33$ to $-11$.
To find how many floors Randall needs to travel past, find the difference between $-5$ and $37$.
SolutionAxel and Tank are in their submarine. They explored the ocean at $35$ m below sea level. They have now descended another $43$ m and are at $\textbf7\textbf8$ m below sea level.
- To solve this problem we need to add $35 + 43 = 78$. We know they are below sea level so we can say they are $78$ m below sea level now.
In a country, the average temperature in winter is $-11$ degrees and the average temperature in summer is $\textbf2\textbf2$ degrees. The difference between these temperatures is $33$ degrees.
- To solve this problem, we needed to add $33$ to $-11$ which equals $22$.
Randall lives on floor $37$ in a skyscraper. The gym is on floor $-5$ so Randall needs to travel down $\textbf4\textbf2$ floors to get there.
- To solve this problem, we need to find the difference between $37$ and $-5$. To do this, we can solve $37 - -5 = 42$.

Rational Numbers on the Number Line
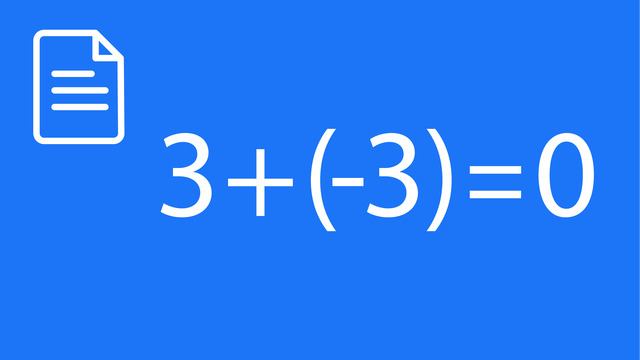
Subtracting Integers

Solving Problems with Negative Numbers
Multiplying and Dividing Integers

Rational and Irrational Numbers
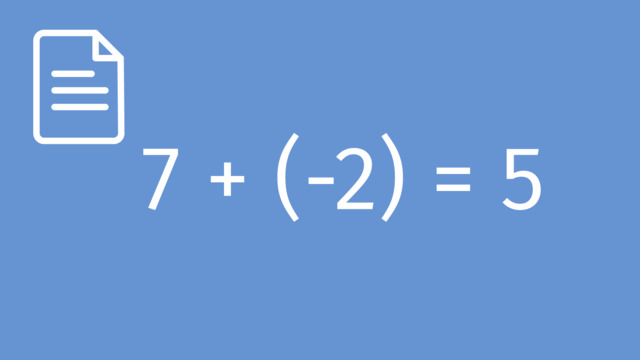
Subtracting Rational Numbers by adding the Inverse

Analysing Numerical Patterns
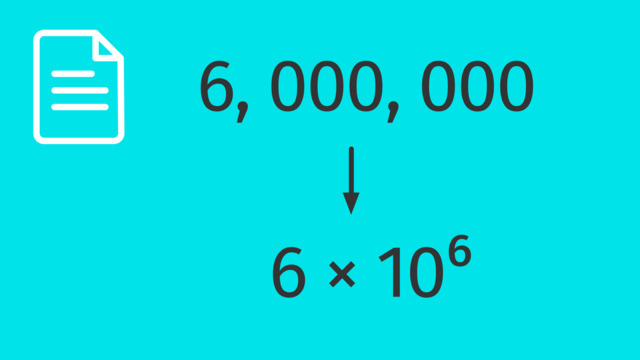
Standard and Scientific Notation
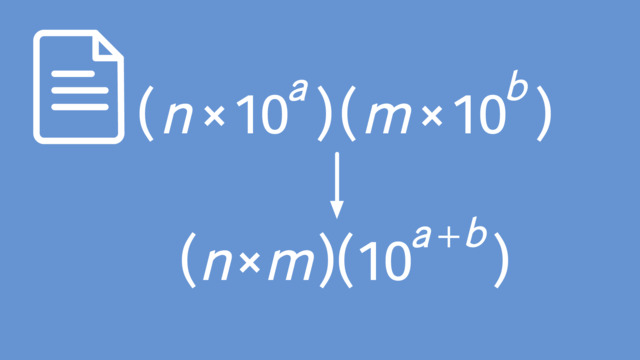
Using Operations with Scientific Notations
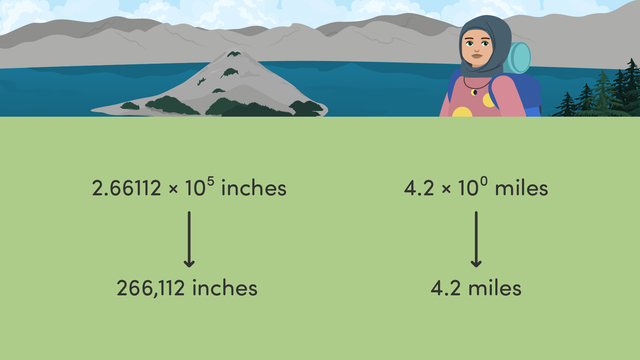
Interpreting Scientific Notation
 Do you want to learn faster and more easily?
Do you want to learn faster and more easily?














