Adding Mixed Numbers with Unlike Denominators
- Adding Mixed Numbers and Unlike Denominators
- Adding Mixed Numbers and Unlike Denominators – Definition
- Converting Mixed Numbers to Improper Fractions
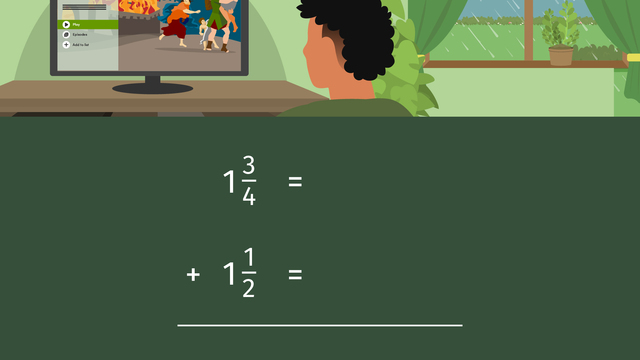

Basics on the topic Adding Mixed Numbers with Unlike Denominators
Adding Mixed Numbers and Unlike Denominators
When we dive into the world of fractions, we encounter different forms that numbers can take. Among these are mixed numbers and fractions with unlike denominators. These concepts are crucial for understanding advanced arithmetic operations and problem-solving in mathematics.
Adding Mixed Numbers and Unlike Denominators – Definition
Mixed numbers are those that consist of a whole number and a fraction combined, such as $2 \frac{3}{4}$. They are especially common in everyday life – think of recipes, measurements and timekeeping.
Converting Mixed Numbers to Improper Fractions
To perform calculations with mixed numbers, such as addition or subtraction, we often need to convert them into improper fractions, where the numerator (the top number) is larger than the denominator (the bottom number).
Adding Mixed Numbers and Unlike Denominators – Explanation
When dealing with fractions, unlike denominators refer to two or more fractions that have different numbers at the bottom. Unlike denominators must be made the same, or common, before we can add or subtract the fractions.
| Step | Description | Details |
|---|---|---|
| 1 | Convert each mixed number into an improper fraction. | $1 \frac{2}{3}$ becomes $\frac{5}{3}$ $2 \frac{1}{4}$ becomes $\frac{9}{4}$ |
| 2 | Find the lowest common denominator (LCD) for the fractions. | LCD for $\frac{5}{3}$ and $\frac{9}{4}$ |
| 3 | Add the improper fractions and simplify if necessary. | Add $\frac{5}{3}$ and $\frac{9}{4}$, simplify the result |
Adding Mixed Numbers with Unlike Denominators – Exercises
Mixed Numbers and Unlike Denominators – Summary
Key Learnings from this Text:
Mixed numbers combine a whole number with a fractional part.
Unlike denominators in fractions need to be converted to a common denominator before performing addition or subtraction.
To work with mixed numbers in calculations, first convert them to improper fractions.
Practice with more examples and explore our resources to further develop your understanding of mixed numbers and unlike denominators.
Mixed Numbers and Unlike Denominators – Frequently Asked Questions
Transcript Adding Mixed Numbers with Unlike Denominators
Today is the perfect day! The pouring rain gives us the best excuse to stay indoors. And what's even more exciting? The long-awaited new season of, "Demise," has just been released! Time to binge-watch before the spoilers come in and ruin it! We can track how much time we spend watching our favourite show by adding mixed numbers with unlike denominators. Time can be converted into mixed numbers that show fractional amounts that represent parts of a whole, as in hours, or in minutes that represent a portion of an hour. We can add fractional amounts of time to determine the time spent on an activity, like binge watching a series. Let's say it took us one and three-quarter hours to watch episode one, and one and a half hours for episode two. We set up the problem like this. To add these mixed numbers, we can convert them to improper fractions. Starting with this fraction, we multiply the denominator, four, by one, and add three to get seven-quarters. In this fraction, we multiply the two by one and add one to get three halves. Now we need to find the lowest common denominator of four and two, which is four. Seven quarters would remain the same, and we would multiply three-halves by two. The renamed fraction is six-quarters. To add these fractions, we bring down the denominator, and add the numerators to get thirteen-quarters. We need to convert this improper fraction back to a mixed number. We do this by dividing the denominator into the numerator. Four goes into thirteen three times, so this becomes our whole number. Four times three is twelve, and thirteen take away twelve is one. One becomes the numerator, and the denominator, four, remains the same. The episodes were watched in three and one-quarter hours. Back to the show for two and three-quarter hours, and after a snack break, one and one-third hours more. What is the total numbers of hours spent on episodes three and four? Let's walk through this one together. You can pause the video at any point if you need extended time. First, convert the mixed numbers to improper fractions. What are the renamed fractions? Eleven-quarters and four-thirds. Now find the least common denominator of four and three. Twelve. What are the renamed fractions with the new numerators? Thirty-three twelfths, sixteen-twelfths. What do you get when you add the fractions? Forty-nine twelfths. And now convert it back to a mixed number by dividing the denominator into the numerator. Four and one-twelfth. What is the final answer for time spent? Four and one-twelfth hours.
Adding Mixed Numbers with Unlike Denominators exercise
-
Can you convert these times to mixed numbers?
HintsThe minutes represent part of an hour. There are 60 minutes in one hour so start by putting the number of minutes over 60.
For example, 30 minutes would be $\frac{30}{60}$.
Simplify the fractions by finding a common factor.
1 hour 30 minutes is equal to $1 \frac{30}{60}$.
If you divide both 30 and 60 by 30, what is the simplified fraction?
Solution- 1 hour 30 minutes = $1 \frac{30}{60}$ = $1 \frac{1}{2}$
- 2 hours 20 minutes = $2 \frac{20}{60}$ = $2 \frac{1}{3}$
- 2 hours 35 minutes = $2 \frac{35}{60}$ = $2 \frac{7}{12}$
- 1 hour 12 minutes = $1 \frac{12}{60}$ = $1 \frac{1}{5}$
-
How long has Luis been watching TV for?
HintsThe addition problem is:
$1 \frac{1}{12} + 1 \frac{3}{4}$
We can convert these mixed numbers to improper fractions to help with addition.
$1 \frac{1}{12}$ $+$ $1 \frac{3}{4}$
is equal to
$\frac{13}{12}$ $+$ $\frac{7}{4}$
Now find a common denominator.
$\frac{13}{12}$ $+$ $\frac{7}{4}$
is equal to
$\frac{13}{12}$ $+$ $\frac{21}{12}$
$\frac{13}{12}$ $+$ $\frac{21}{12}$ $=$ $\frac{34}{12}$
Convert $\frac{34}{12}$ to a mixed number and simplify.
SolutionThe correct answer is $2 \frac{5}{6}$ hours.
$1 \frac{1}{12} + 1 \frac{3}{4}$
is equal to
$\frac{13}{12} + \frac{7}{4}$
is equal to
$\frac{13}{12} + \frac{21}{12} = \frac{34}{12} = 2 \frac{10}{12} = 2 \frac{5}{6}$
-
Which two programmes has Luis watched?
HintsStart by converting $2 \frac{5}{6}$ to an improper fraction.
$2 \frac{5}{6} = \frac{17}{6}$ or $\frac{34}{12}$
Now convert all of the programme times to improper fractions.
Which two would add together to equal $\frac{34}{12}$?
- Football Today = $\frac{20}{12}$
- Laughathon = $\frac{26}{12}$
- The Pinnacle = $\frac{13}{12}$
- The Ultimate Game Show = $\frac{14}{12}$
SolutionThe correct answers are Football Today and The Ultimate Game Show.
Luis has been watching TV for $2 \frac{5}{6}$ hours which is equal to $\frac{17}{6}$ or $\frac{34}{12}$.
If we convert all of the programme time lengths to improper fractions with a denominator of $12$ we get:
- Football Today = $\frac{20}{12}$
- Laughathon = $\frac{26}{12}$
- The Pinnacle = $\frac{13}{12}$
- The Ultimate Game Show = $\frac{14}{12}$
We can see that if we add Football Today = $\frac{20}{12}$ + The Ultimate Game Show = $\frac{14}{12}$ we get $\frac{34}{12}$.
-
Which programmes could Luis watch if he had exactly $2 \frac{5}{12}$ hours?
HintsWhat is $2 \frac{5}{12}$ as in improper fraction?
Convert all of the programme lengths to improper fractions.
Make sure all of the improper fractions have the same denominator.
Which two programmes add together to equal $2 \frac{5}{12}$ as in improper fraction?
There are two programmes to highlight.
SolutionThe correct answers are The Home Show and The Seven Seas.
The total amount of time Luis had was $2 \frac{5}{12}$ or $\frac{29}{12}$.
The programme lengths are:
- Cricket : $2 \frac{1}{12}$ hours = $\frac{25}{12}$
- The Home Show : $1 \frac{1}{6}$ hours = $\frac{7}{6}$ or $\frac{14}{12}$
- The Seven Seas : $1 \frac{1}{4}$ hours = $\frac{5}{4}$ or $\frac{15}{12}$
- History and More : $1 \frac{7}{12}$ hours = $\frac{19}{12}$
- News Special : $1 \frac{2}{3}$ hours = $\frac{5}{3}$ or $\frac{20}{12}$
The only two programmes that add up to $\frac{29}{12}$ are The Home Show $\frac{14}{12}$ and The Seven Seas $\frac{15}{12}$.
-
Complete the addition problem.
HintsFirst, convert the mixed numbers to improper fractions.
- $1 \times 6 = 6 + 5 = 11$ therefore $1 \frac{5}{6} = \frac{?}{6}$
- $3 \times 3 = 9 + 1 = 10$ therefore $3 \frac{1}{3} = \frac{?}{3}$
$3 \frac{1}{3} = \frac{10}{3} = \frac{?}{6}$
We multiplied the denominator $3$ by two to get $6$, so multiply the numerator $10$ by two as well.
$\frac{11}{6} + \frac{20}{6} = \frac{?}{6}$
Convert this answer to a mixed number.
SolutionHere we can see the completed addition problem.
We first needed to convert the mixed numbers to improper fractions:
- $1 \times 6 = 6$
- $6 + 5 = 11$ therefore $1 \frac{5}{6} = \frac{11}{6}$
- $3 \times 3 = 9$
- $9 + 1 = 10$ therefore $3 \frac{1}{3} = \frac{10}{3}$
$\frac{11}{6} + \frac{20}{6} = \frac{31}{6} = 5 \frac{1}{6}$
-
Can you solve the addition problems?
HintsYou can convert the mixed numbers to improper fractions to solve or you can add the whole numbers and add the fractions separately.
For example, when solving $6 \frac{4}{5} + 4 \frac{4}{15}$ we can add $6 + 4 = 10$ and then add $\frac{4}{5} + \frac{4}{15}$.
$\frac{4}{5} + \frac{4}{15} = \frac{12}{15} + \frac{4}{15} = \frac{16}{15} = 1 \frac{1}{15}$
Add $10 + 1$ $\frac{1}{15} = 11 \frac{1}{15}$
Solution- $6 \frac{4}{5} + 4 \frac{4}{15} = 11 \frac{1}{15}$
- $6 \frac{13}{18} + 5 \frac{1}{9} = 11 \frac{5}{6}$
- $8 \frac{7}{12} + 3 \frac{1}{4} = 11 \frac{5}{6}$
- $2 \frac{1}{5} + 10 \frac{4}{10} = 12 \frac{3}{5}$
- $7 \frac{2}{5} + 5 \frac{3}{15} = 12 \frac{3}{5}$
- $2 \frac{1}{6} + 4 \frac{1}{18} = 6 \frac{2}{9}$
Adding Fractions
Adding Tenth and Hundredth

Adding Tenth and Hundredth — Let's Practise!
Adding Fractions on a Number Line
Adding Fractions on a Number Line- Let's Practise!
Subtracting Fractions on a Number Line
Subtracting Fractions on a Number Line — Let's Practise
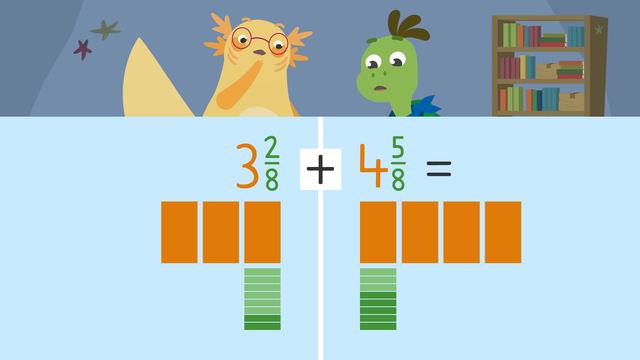
Adding and Subtracting Mixed Numbers

Adding and Subtracting Mixed Numbers with Common Denominators—Let's Practise!

Adding Fractions with Different Denominators
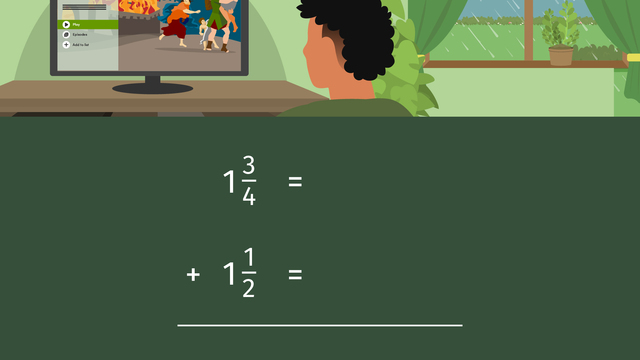
Adding Mixed Numbers with Unlike Denominators
 Do you want to learn faster and more easily?
Do you want to learn faster and more easily?









