Adding and Subtracting Mixed Numbers
Basics on the topic Adding and Subtracting Mixed Numbers
How Do You Add and Subtract Mixed Numbers?
Have you ever tried making slime at home? It is a lot of fun!
For the special slime we want to make today, the recipe is difficult to read, as it contains mixed numbers. In order to work out how much to use of each ingredient, we need to learn and practise adding and subtracting mixed numbers. Not to worry – the following text teaches us everything we need to know.
Steps to Adding and Subtracting Mixed Numbers
A mixed number is a combination of a whole number and a fraction. When you practise adding and subtracting mixed numbers with like denominators, you can follow these three steps:
- Step One: Add or subtract the whole numbers.
- Step Two: Add or subtract the fractions.
- Step Three: Simplify your answer if you need to.
Adding and Subtracting Mixed Numbers – Examples
The first ingredient on the recipe is glue. It says to add three and two-eighths plus four and five-eighths. What is that in total? Let’s start by adding three and two-eighths and four and five-eighths.
First, we need to find the sum of the whole numbers. That means, we are adding three and four first to get the sum of seven.
Next, we find the sum of the fractions.
Remember: When adding and subtracting fractions with common denominators, we simply add or subtract the numerators and the denominators stay the same. Here, this means two-eighths plus five-eighths equals seven-eighths.
Our last step is to simplify our answer if we need to. A fraction is in simplest form when the numerator and denominator have no common factors other than one. Since seven and seven-eighths is in simplest form we can skip this step.
What is the next ingredient on the slime recipe? Now, we have to add five and three-quarters minus four and one-quarter of baking soda. So let’s practise subtracting mixed numbers by calculating five and three-quarters minus four and one-quarter.
First, we need to find the difference of the whole numbers. That means, we are subtracting five and four first to get the difference of one.
Next, we find the difference of the fractions. Three-quarters minus one-quarter equals two-quarters.
Our last step is again to simplify our answer if we need to. The numerator and the denominator have the common factor of two, which means it can be simplified to one-half.
How to Add and Subtract Mixed Numbers – Summary
Remember to follow the three steps above whenever you add and subtract mixed numbers with like denominators.
The last step in our recipe is to add one and one-third plus two and two-thirds of contact lens solution. Can you calculate how much that is in total?
The answer is... four! Well done.
If you would like to practise some more to optimise your slime, take a look at the practise problems and worksheets about adding and subtracting mixed numbers. Enjoy!
Transcript Adding and Subtracting Mixed Numbers
Axel and Tank are having a lazy day. Tank decides he wants to read a book, but what is this? Looks like some kind of recipe...very mysterious! In order to figure out what the recipe makes, Tank and Axel need to add and subtract mixed numbers so they know how much of each ingredient to use. A mixed number is a combination of a whole number and a fraction. Remember, a fraction is made up of a numerator and denominator and represents a part of a whole. We can add or subtract mixed numbers using three steps. The first step is to add or subtract the whole numbers. The second step is to add or subtract the fractions. The third step is to simplify your answer if you need to. Let's see how many containers of glue Axel and Tank need. In order to do that, we need to add three and two-eighths and four and five-eighths. First, we need to find the sum of the whole numbers. That means, we are adding three and four first. What is the sum of three plus four? The sum of three and four is seven. Next, we find the sum of the fractions. Remember, when we add or subtract fractions with common denominators we simply add or subtract the numerators and the denominators stay the same. Two-eighths plus five-eighths equals seven-eighths. Our last step is to simplify our answer if we need to. A fraction is in its simplest form when the numerator and denominator have no common factors, other than one. This is true for the fraction seven-eighths, so they need seven and seven-eighths containers of glue. Now, let's help them calculate how many containers of baking soda they need. In order to do that, we need to subtract four and one-quarter from five and three-quarters. First, we need to find the difference of the whole numbers. So, what is the difference of the whole numbers when you subtract? When we subtract the whole number four from five the difference is one. Next, we subtract the fractions. What is the difference of the fractions three-quarters and one-quarter? Since the denominators stay the same, we only subtract three minus one. Three minus one is two which gives us the final answer two-quarters. Our last step is to simplify our answer if we need to. Can we simplify the fraction two-quarters? The numerator and the denominator have the common factor of two, which means it can be simplified to one-half. Axel and Tank need one and one-half containers of baking soda for the recipe. Lastly, let's help them calculate how many containers of contact lens solution they need. In order to do that, we need to add one and one-third and two and two-thirds. First, can you find the sum of the whole numbers by adding? The sum of one plus two is three. Next, we add the fractions. What is the sum of the fractions? The sum of one-third plus two thirds is three-thirds. Our last step is to simplify our answer if we need to. Can we simplify the fraction three-thirds? Since we have all three parts of our whole we can rewrite three-thirds as one whole. Now we add three plus one which gives us four. Axel and Tank need four containers of contact lens solution for the recipe. Remember, you can add or subtract mixed numbers with common denominators by following three steps. The first step is to add or subtract the whole numbers. The second step is to add or subtract the fractions. The third step is to simplify your answer if you need to. Luckily, Axel and Tank had enough of each ingredient to hand. Let's see how the recipe turned out!
Adding and Subtracting Mixed Numbers exercise
-
Can you find the mixed numbers?
HintsIs it made up of a whole number and a fraction?
Remember, a mixed number is made up of a whole number and a fraction.
SolutionThese are the mixed numbers! Remember, a mixed number is made up of a whole number and a fraction.
Not mixed numbers
5 and 13 are whole numbers.
$\frac{9}{10}$ and $\frac{5}{7}$ are fractions.
-
Can you sequence the number sentence correctly?
HintsThis is a subtraction problem so the order is important.
Start with the biggest number.
Remember, answers may be simplified.
Have a look at this fraction. If you divide both the numerator and the denominator by 2, what do you get?
SolutionThis is how the number sentence should read.
First of all we subtract the whole numbers so 3 - 1 = 2.
We then subtract the fractions so $\frac{3}{4}$ - $\frac{1}{4}$ = $\frac{2}{4}$.
We then simplify if we need to which in this case we can. $\frac{2}{4}$ can be simplified to $\frac{1}{2}$ by dividing both the numerator and the denominator by two.
We then put the whole number and the fraction together to get our answer of 2$\frac{1}{2}$.
-
Can you find out how much of each ingredient Axel and Tank need to make gloop?
HintsCan it be simplified?
Add or subtract the whole numbers first.
Add or subtract the fractions next.
Don't forget to double check if it is an addition or subtraction problem.
SolutionThese are the correct answers. Remember to:
- Check whether it is an addition or subtraction problem.
- Add or subtract the whole numbers first.
- Add or subtract the fractions next.
- Simplify if you can.
-
Can you find the equivalent fractions?
HintsRemember, you always divide the numerator and the denominator by the same number.
Think about common factors.
What do you get if you half the denominator on the top row? Or divide it by 3?
In this example we can simplify $\frac{3}{6}$ to $\frac{1}{2}$ by dividing both the numerator and denominator by 3.
SolutionIn the example above, both the numerator and the denominator have been divided by two to simplify the fraction.
You need to divide the denominator and the numerator by the same number to simplify the fraction. This may be by two or by three, or by another number.
__________________________________________________________________
Using the information above, the answers to the other problems are:
- $5\frac{8}{10}$ = $5\frac{4}{5}$ - both divided by two.
- $5\frac{3}{9}$ = $5\frac{1}{3}$ - both divided by three.
- $5\frac{12}{16}$ = $5\frac{3}{4}$ - both divided by four.
-
Can you find out how much shaving foam Axel and Tank need to make more slime?
HintsRemember to add the whole numbers first.
Add the fractions next.
When the denominators are the same, we only need to add the numerators.
SolutionIf we add the whole numbers first we get 3.
Adding the fractions next gives us $\frac{2}{3}$; we cannot simplify this any further.
-
Can you check Axel and Tank's alternative recipe for slime?
HintsRemember to add or subtract the whole numbers first.
Add or subtract the fractions next.
Can the fraction be simplified?
Solution- The first number sentence was incorrect.
3 + 6 = 9
$\frac{5}{8}$ + $\frac{1}{8}$ = $\frac{6}{8}$ which can be simplified to $\frac{3}{4}$.
We put the whole number and the fraction together to get the answer.
- The second problem was correct!
$\frac{7}{9}$ + $\frac{2}{9}$ = 1.
8 + 1 = 9.
- The third number sentence was also incorrect.
10 - 7 = 3.
$\frac{6}{7}$ - $\frac{2}{7}$ = $\frac{4}{7}$.
This cannot be simplified further so put the whole number and the fraction together to get the answer.
- The fourth number sentence was correct!
$\frac{7}{8}$ - $\frac{3}{8}$ = $\frac{4}{8}$ which can be simplified to $\frac{1}{2}$.
Put the whole number and the fraction together to get the answer.
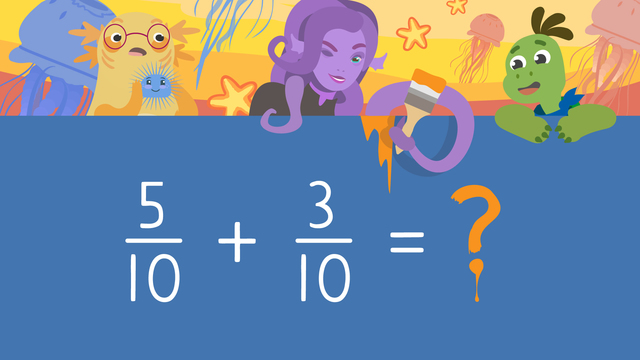
Adding Fractions
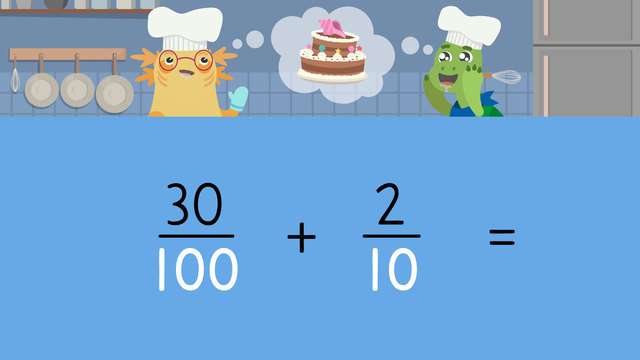
Adding Tenth and Hundredth

Adding Tenth and Hundredth — Let's Practise!
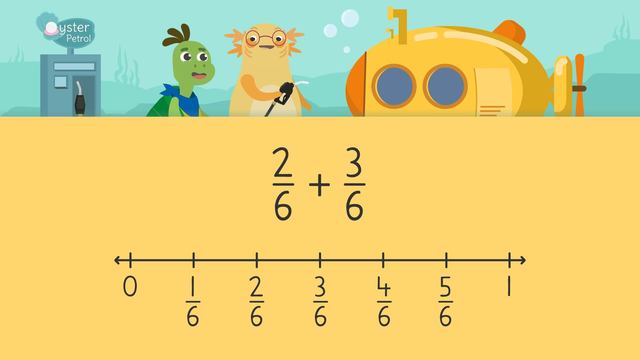
Adding Fractions on a Number Line
Adding Fractions on a Number Line- Let's Practise!
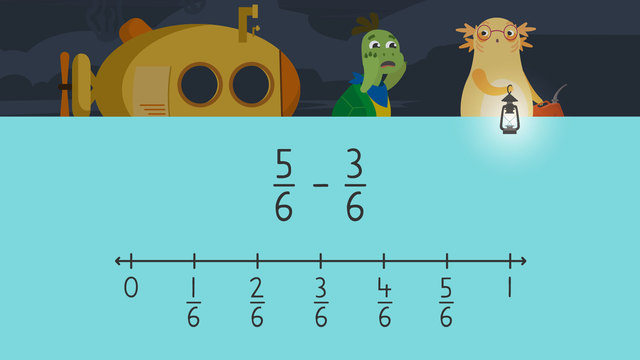
Subtracting Fractions on a Number Line
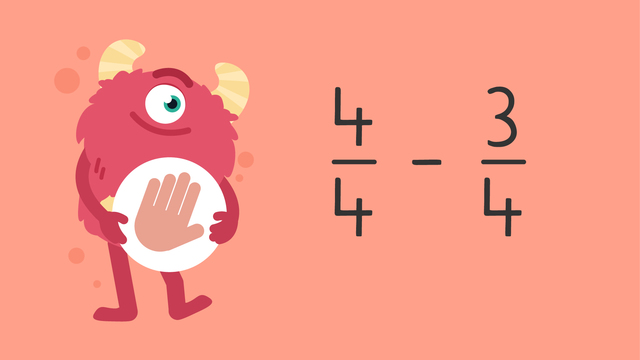
Subtracting Fractions on a Number Line — Let's Practise
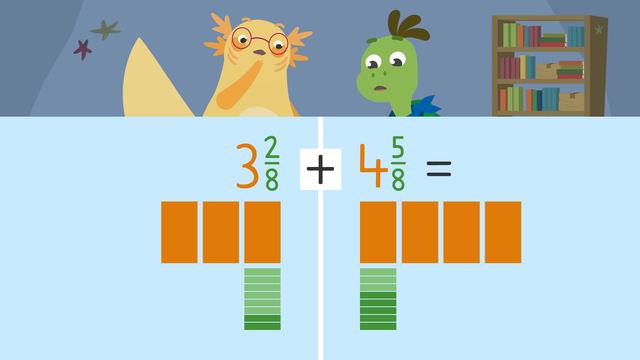
Adding and Subtracting Mixed Numbers

Adding and Subtracting Mixed Numbers with Common Denominators—Let's Practise!

Adding Fractions with Different Denominators
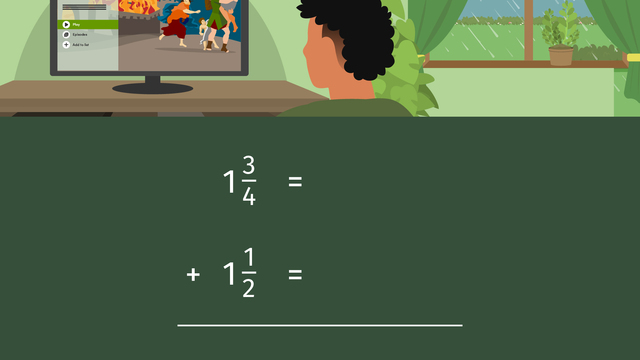
Adding Mixed Numbers with Unlike Denominators

 Do you want to learn faster and more easily?
Do you want to learn faster and more easily?














