Adding and Subtracting Mixed Numbers with Common Denominators—Let's Practise!


Basics on the topic Adding and Subtracting Mixed Numbers with Common Denominators—Let's Practise!
Adding and Subtracting Mixed Numbers with Common Denominators – Introduction
We're diving into the world of adding and subtracting mixed numbers with common denominators. These problems require us to work with both whole numbers and fractions. As we embark on this mathematical journey, remember that solving these problems is like unraveling a mystery, and you're the detective!
What Are Mixed Numbers?
Mixed numbers are numbers that contain both a whole number and a fraction. When adding or subtracting mixed numbers, we need to handle the whole numbers and fractions separately. First, we gather clues by reading the problem carefully. Then, we use mathematical operations as our tools to solve the mystery.
Here are the steps to tackle adding and subtracting mixed numbers with common denominators:
| Step # | Action |
|---|---|
| 1 | Read the problem and determine what you are asked to find. |
| 2 | Identify the whole numbers and fractions. |
| 3 | Add or subtract the whole numbers. |
| 4 | Add or subtract the fractions. |
| 5 | Simplify the fraction if necessary. |
| 6 | Combine the whole number and fraction to get the final answer. |
| 7 | Check your answer to ensure it makes sense with the problem. |
Let's practise understanding mixed number problems with a couple of exercises.
Solving Mixed Number Problems – Example
Example 1:
Problem: Solve $2\frac{3}{7}+4\frac{2}{7}$
Steps to Solve the Problem:
| Step # | Action | Equation |
|---|---|---|
| 1 | Write an equation for the problem. | $2\frac{3}{7} + 4 \frac{2}{7}$ |
| 2 | Add the whole numbers. | $2 + 4 = 6$ |
| 3 | Add the fractions. | $\frac{3}{7}$ + $\frac{2}{7}$ = $\frac{5}{7}$ |
| 4 | Combine the whole number and fraction. | $6\frac{5}{7}$ |
Solution: The sum is $6\frac{5}{7}$.
Example 2:
Problem: Solve $5\frac{8}{10} - 1\frac{3}{10}$.
Steps to Solve the Problem:
| Step # | Action | Equation |
|---|---|---|
| 1 | Write an equation for the problem. | $5\frac{8}{10} - 1\frac{3}{10}$ |
| 2 | Subtract the whole numbers. | $5 - 1 = 4$ |
| 3 | Subtract the fractions. | $\frac{8}{10}$ - $\frac{3}{10}$ = $\frac{5}{10}$ |
| 4 | Simplify the fraction if necessary. | $\frac{5}{10}$ = $\frac{1}{2}$ |
| 5 | Combine the whole number and fraction. | $4\frac{1}{2}$ |
Solution: The difference is $4\frac{1}{2}$.
Example 3:
Problem: Solve $3\frac{1}{2} + 3\frac{1}{2} + 4$.
Steps to Solve the Problem:
| Step # | Action | Equation |
|---|---|---|
| 1 | Write an equation for the problem. | $3\frac{1}{2} + 3\frac{1}{2} + 4$ |
| 2 | Add the whole numbers. | $3 + 3 + 4 = 10$ |
| 3 | Add the fractions. | $\frac{1}{2}$ + $\frac{1}{2}$ = $\frac{2}{2}$ |
| 4 | Simplify the fraction if necessary. | $\frac{2}{2} = 1$ |
| 5 | Combine the whole number and fraction. | $10 + 1 = 11$ |
Solution: The sum is $11$.
Solving Mixed Number Problems – Practice
Now, let's put your skills to the test. Solve these problems on your own and check the solutions when you're ready!
Solving Mixed Number Problems – Summary
Key Learnings from this Text:
- Solving problems with mixed numbers can be achieved by following these steps:
| Step # | Action |
|---|---|
| 1 | Read the problem and determine what you are asked to find. |
| 2 | Identify the whole numbers and fractions. |
| 3 | Add or subtract the whole numbers. |
| 4 | Add or subtract the fractions. |
| 5 | Simplify the fraction if necessary. |
| 6 | Combine the whole number and fraction to get the final answer. |
| 7 | Check your answer to ensure it makes sense with the problem. |
- Mastering mixed number addition and subtraction is an important skill in mathematics.
Keep practising these steps and you'll become a pro at solving mixed number problems! Check out more fun maths challenges and exercises on our website to continue sharpening your skills.
Solving Mixed Number Problems – Frequently Asked Questions
Transcript Adding and Subtracting Mixed Numbers with Common Denominators—Let's Practise!
Razzi says get these items ready because today we're going to practise adding and subtracting mixed numbers with the same denominator. It's time to begin! Solve two and three-sevenths plus four and two-sevenths. Pause the video to work on the problem and press play when you are ready to see the solution! First add the whole numbers to get six, then add the fractions to get five-sevenths! Did you also get six and five-sevenths? Let's tackle the next problem! Solve five and eight-tenths minus one and three tenths. Pause the video to work on the problem and press play when you are ready to see the solution! First subtract the whole numbers to get four, then subtract the fractions to get five-tenths! Simplify five tenths by dividing the numerator and denominator by five, to get one half. Did you also get four and a half? Let's practise one more! Solve three and one-half plus three and one-half plus four. Pause the video to work on the problem and press play when you are ready to see the solution! First add the whole numbers to get ten then add the fractions to get two halves. Two halves is the same as one whole, so add one more to get eleven! Did you also get eleven as your answer? Razzi had so much fun practising with you today! See you next time!
Adding and Subtracting Mixed Numbers with Common Denominators—Let's Practise! exercise
-
Workout the fraction problems using addition or subtraction.
HintsFirst, we need to add the whole number.
Next, we add across our numerators.
Lastly, as the denominators (bottom number) are the same, our answer should have the same too. Remember, sometimes our answers can be simplified.
Has your answer been simplified?
In this example $\frac{1}{4}$ + $\frac{1}{4}$ = $\frac{2}{4}$
$\frac{2}{4}$ can be simplified. Both the numerator and denominator can be divided by 2, so our answer would be simplified from $\frac{2}{4}$ to $\frac{1}{2}$
$\frac{1}{4}$ + $\frac{1}{4}$ = $\frac{1}{2}$
Use the images to help you. You can count the whole cakes and the slices.
Solution2 $\frac{3}{5}$ + 1 $\frac{1}{5}$ = 3 $\frac{4}{5}$
1 $\frac{1}{4}$ + 3 $\frac{2}{4}$ = 4 $\frac{3}{4}$
2 $\frac{1}{2}$ + 2$\frac{1}{2}$ = 5
1 $\frac{2}{6}$ + 1 $\frac{1}{6}$ = 2 $\frac{1}{2}$
-
Solve the addition and subtraction fraction problems
HintsFirst, we add or subtract the whole numbers.
Next we add or subtract the numerators top numbers.
When the denominators bottom number are the same in the question, they will also be the same for the answer.
Solution2 $\frac{2}{6}$ + 2 $\frac{3}{6}$ = 4$\frac{5}{6}$
2 $\frac{3}{6}$ - 1 $\frac{2}{6}$ = 1 $\frac{1}{6}$
2 $\frac{1}{4}$ + 3 $\frac{2}{4}$ = 5 $\frac{3}{4}$
1 $\frac{2}{3}$ - 1 $\frac{1}{3}$ = $\frac{1}{3}$
-
Addition and subtraction
HintsFirstly, we need to add or subtract the whole numbers. How many whole cakes are there?
Next, we need to add or subtract the numerator. The numerator refers to the parts we have (slices of cake)
The denominator bottom number is how many parts the cake has been split into.
Solution1 $\frac{1}{3}$ + 1 $\frac{1}{3}$ = 2 $\frac{2}{3}$
2 $\frac{1}{4}$ - $\frac{3}{4}$ = 1 $\frac{1}{2}$
1 $\frac{2}{6}$ + 2 $\frac{3}{6}$ = 3 $\frac{5}{6}$
2 $\frac{4}{5}$ - 2$\frac{3}{5}$ = $\frac{1}{5}$
-
Solve the fraction problems.
HintsFirst, look to see what you need to do. Is it an addition or a subtraction question?
When you have done this, you can then add or subtract the whole numbers.
Then, look at the numerators and either add or subtract these.
Finally, look at the denominator bottom number. This will be the same for the answer. So we can write this in the blank denominator space.
Solution2 $\frac{1}{5}$ + 3 $\frac{2}{5}$ = 5 $\frac{3}{5}$
3 $\frac{5}{7}$ - 1 $\frac{4}{7}$ = 2 $\frac{1}{7}$
4 $\frac{2}{7}$ - 1 $\frac{1}{7}$ = 3 $\frac{1}{7}$
1 $\frac{2}{5}$ + 1$\frac{3}{5}$ = 3
-
Solve the equation to create a new fraction.
HintsFirst, we need to add the whole numbers, which are also shown as the whole pizzas. Then add this to the whole number box.
Next, we can add the parts of the fraction, these are the slices of pizza. Put your answer in the numerator top number box.
How many slices has the pizza been split into? This is our denominator bottom number.
Solution2 $\frac{1}{3}$ + 1 $\frac{1}{3}$ = 3 $\frac{2}{3}$
-
Work out the missing numbers.
HintsLook at the questions. If the denominator bottom number is blank, we can look at the denominators in the question as they will all be the same.
If the numerator (top number) is blank, we can use the inverse to help work it out. Look at this example.
Solution2 $\frac{2}{4}$ + 1 $\frac{1}{4}$ = 3 $\frac{3}{4}$
2 $\frac{5}{7}$ - 1 $\frac{2}{7}$ = 1 $\frac{3}{7}$
1 $\frac{2}{5}$ + 2 $\frac{2}{5}$ = 3 $\frac{4}{5}$
4 $\frac{2}{3}$ - 2 $\frac{1}{3}$ = 2 $\frac{1}{3}$
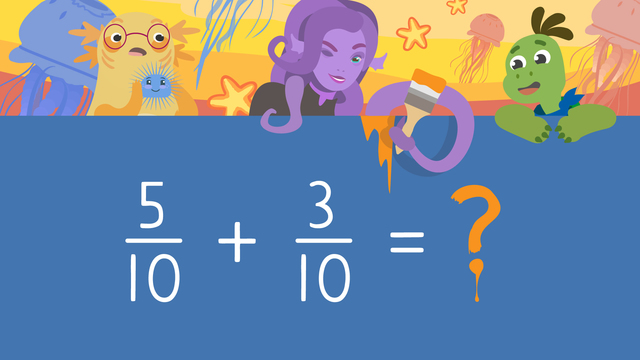
Adding Fractions
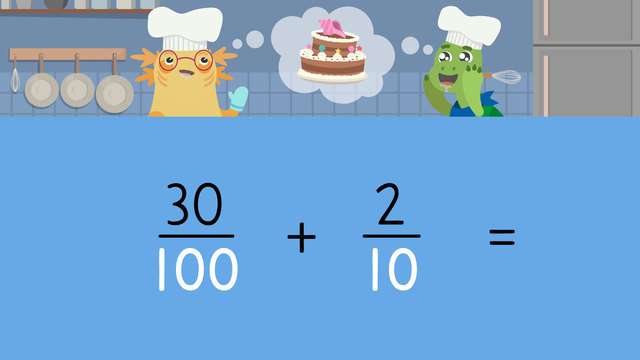
Adding Tenth and Hundredth

Adding Tenth and Hundredth — Let's Practise!
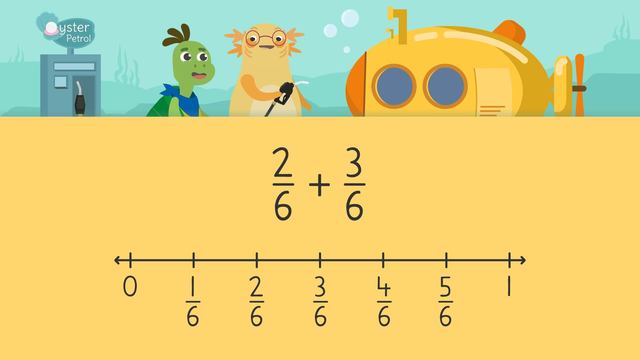
Adding Fractions on a Number Line
Adding Fractions on a Number Line- Let's Practise!
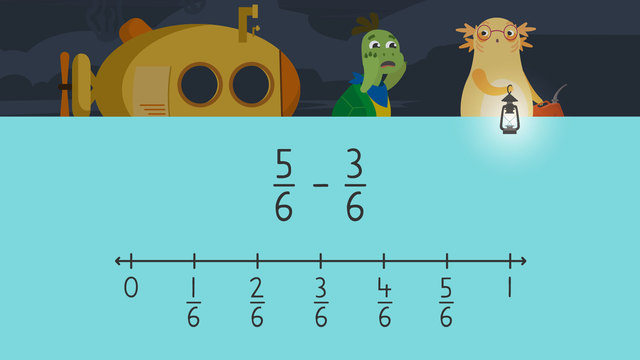
Subtracting Fractions on a Number Line
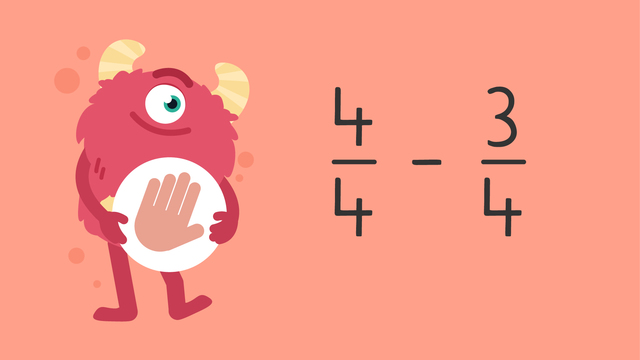
Subtracting Fractions on a Number Line — Let's Practise
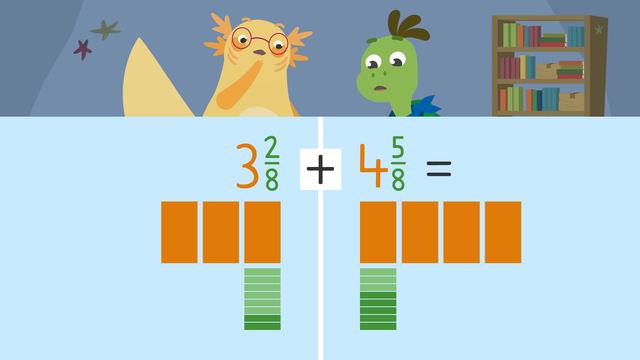
Adding and Subtracting Mixed Numbers

Adding and Subtracting Mixed Numbers with Common Denominators—Let's Practise!

Adding Fractions with Different Denominators
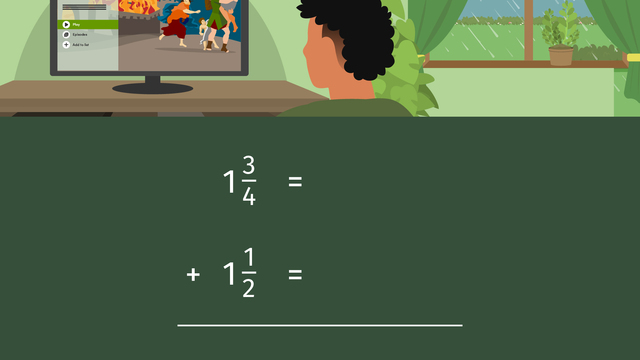
Adding Mixed Numbers with Unlike Denominators
 Do you want to learn faster and more easily?
Do you want to learn faster and more easily?









