Adding Fractions with Different Denominators


Basics on the topic Adding Fractions with Different Denominators
How do we add fractions with different denominators? Learn here about converting the fractions to have the same denominator so that they are easier to add together.
Transcript Adding Fractions with Different Denominators
June is preparing to launch her company, Fifi's Fancy Frocks. She is finishing up the final outfits when she realises she only has a few materials left. She will need to add various fractional amounts to determine how much material she has to work with by adding fractions with different denominators. Let's do a quick vocabulary review. The 'lowest common multiple' is the lowest multiple shared by two or more numbers. The 'lowest common denominator' is the lowest number that can be used as the denominator for two or more fractions. The greatest common factor is the largest factor that all the numbers share. Our previous experience with fractions, combined with these terms, will be useful when adding fractions with different denominators. June has two spools of red thread remaining. The first has two-fifths of a metre, while the second has one-third. To see how much red thread there is, we'll add two-fifths and one-third. Before we can add, we must convert the fractions with different denominators into equivalent fractions with a common denominator. We will find the lowest common denominator of five and three by thinking about the lowest common multiple they share. What is the lowest common multiple of five and three? Fifteen. Now, using the common denominator, fifteen, we rename each fraction. To do this, we multiply two and five by three, and one and three by five. We now have six-fifteenths and five-fifteenths. These fractions can now be added. We bring down the denominator, fifteen, because the number of equal parts does not change and add the numerators to get eleven. Two-fifths plus one-third equals eleven-fifteenths. Eleven-fifteenths cannot be simplified because eleven and fifteen share only one factor. June has eleven-fifteenths of a metre of the red thread. She also has enough cotton to make another shirt. We can calculate the number of metres available by adding three-sixths and two-twelfths. This time, pause to solve the problem and press play when you're ready to review. The lowest common denominator of six and twelve is twelve. Because we multiply the numerator and denominator by two, three-sixths becomes six-twelfths. Two-twelfths remains the same because twelve is already in the denominator. To add, bring down the denominator, twelve and add the numerators, to get eight. The answer is eight-twelfths. Looking at eight-twelfths, we can see that it can be simplified because the numerator and denominator share common factors. Four is the greatest common factor of eight and twelve so they can be divided by four. Eight-twelfths is simplified to two-thirds. June has two-thirds of a metre of cotton. To summarise, before we can add, we must convert fractions with different denominators into equivalent fractions with a common denominator. Then, bring down the denominator add the numerators and, if necessary, simplify the fraction. Fifi's Fancy Frocks is officially open for business!
Adding Fractions with Different Denominators exercise
-
Define the terms.
HintsA denominator is part of a fraction.
Look for common words on the left and right sides to help you make matches.
Think of the word least as small, and the word greatest as large.
Solution- The Lowest Common Multiple, or LCM is the smallest multiple shared by two or more numbers.
- The Lowest Common Denominator, or LCD is the lowest number that can be used as the denominator for two or more fractions.
- The Greatest Common Factor or GCF is the largest factor that all the numbers share.
- The denominator is the number below the fraction bar.
-
Sort the steps.
HintsThe numerator is the number above the fraction bar, and the denominator is the number below.
Before adding fractions with unlike denominators, you need to find a common denominator using multiplication or division.
Example: $\frac{1}{2}$ and $\frac{1}{4}$
$\frac{1}{2}$ = $\frac{2}{4}$ if we multiply the numerator and denominator by 2.
$\frac{2}{4}$ and $\frac{1}{4}$ have common denominators and can now be added together.SolutionThe steps to add fractions with unlike denominators are:
1) Change fractions with unlike denominators to equivalent fractions with a common denominator. ($\frac{1}{12}$ + $\frac{1}{4}$ becomes $\frac{1}{12}$ + $\frac{3}{12}$)
2) Bring the common denominator over to the solution side of the equation ($\frac{1}{12}$ + $\frac{3}{12}$ = $\frac{}{12}$)
3) Add the numerators ($\frac{1}{12}$ + $\frac{3}{12}$ = $\frac{4}{12}$)
4) Simplify the fraction if necessary ($\frac{4}{12}$ becomes $\frac{1}{3}$) -
Add fractions with unlike denominators.
HintsSometimes the lowest common denominator is already the denominator of one of the fractions in the equation.
To find what $\frac{1}{5}$ is equivalent to, we need to multiply the numerator and denominator by 3.
- 1 x 3 = numerator
- 5 x 3 = denominator
You have the solution for $\frac{3}{15}$ + $\frac{2}{15}$ = ? from step 3. Now divide both the numerator and denominator of this fraction by 5 to simplify.
SolutionSTEP ONE
$\frac{1}{5}$ = $\frac{3}{15}$
Now we can add $\frac{3}{15}$ + $\frac{2}{15}$
STEP TWO
$\frac{3}{15}$ + $\frac{2}{15}$ = $\frac{}{15}$
STEP THREE
$\frac{3}{15}$ + $\frac{2}{15}$ = $\frac{5}{15}$
STEP FOUR
$\frac{5}{15}$ = $\frac{1}{3}$ -
Solve the equations.
HintsIn order to add fractions with unlike denominators, first create equivalent fractions with the same denominator using multiplication or division.
Example:
$\frac{1}{5}$ + $\frac{2}{15}$
$\frac{1}{5}$ = $\frac{3}{15}$
$\frac{3}{15}$ and $\frac{2}{15}$ can be added together.Next, bring the common denominator over to the solution side of the equation and add the numerators together.
Example:
$\frac{3}{15}$ + $\frac{2}{15}$ = $\frac{5}{15}$Finally, look for a Greatest Common Factor, and simplify if possible.
Example:
$\frac{5}{15}$ can be simplified to $\frac{1}{3}$ by dividing the numerator and denominator by 5.One of the solutions must be simplified.
Solution1) $\frac{3}{10}$ + $\frac{3}{5}$ = ?
$\frac{3}{10}$ + $\frac{6}{10}$ = $\frac{9}{10}$2) $\frac{1}{4}$ + $\frac{1}{6}$ = ?
$\frac{3}{12}$ + $\frac{2}{12}$ = $\frac{5}{12}$3) $\frac{1}{3}$ + $\frac{2}{9}$ = ?
$\frac{3}{9}$ + $\frac{2}{9}$ = $\frac{5}{9}$4) $\frac{1}{10}$ + $\frac{3}{20}$ = ?
$\frac{2}{20}$ + $\frac{3}{20}$ = $\frac{5}{20}$ = $\frac{1}{4}$ -
Find the lowest common denominator.
HintsThe Lowest Common Denominator, or LCD, is the smallest number that can be used to make equal denominators in fractions.
Example: The LCD for $\frac{1}{4}$ and $\frac{1}{5}$ is 20.Since all of the fractions have even numbers as denominators, the answer cannot be an odd number.
Try multiplying the greatest denominator (8) by 2, and see if the other denominators can fit into the solution. If not, the answer must be a greater number.
Solution- 4 x 6 = 24
- 6 x 4 = 24
- 8 x 3 = 24
-
Solve the equations.
HintsIn order to add fractions with unlike denominators, first create equivalent fractions with the same denominator using multiplication or division.
Example:
$\frac{1}{5}$ + $\frac{2}{15}$
$\frac{1}{5}$ = $\frac{3}{15}$
$\frac{3}{15}$ and $\frac{2}{15}$ can be added together.Next, bring the common denominator over to the solution side of the equation and add the numerators together.
Example:
$\frac{3}{15}$ + $\frac{2}{15}$ = $\frac{5}{15}$Finally, look for a Greatest Common Factor, and simplify if possible.
Example:
$\frac{5}{15}$ can be simplified to $\frac{1}{3}$ by dividing the numerator and denominator by 5.Three of the solutions must be simplified.
Solution1) $\frac{3}{9}$ + $\frac{1}{3}$ = ?
$\frac{3}{9}$ + $\frac{3}{9}$ = $\frac{6}{9}$ = $\frac{2}{3}$2) $\frac{1}{6}$ + $\frac{2}{12}$ = ?
$\frac{2}{12}$ + $\frac{2}{12}$ = $\frac{4}{12}$ = $\frac{1}{3}$3) $\frac{1}{8}$ + $\frac{3}{16}$ = ?
$\frac{2}{16}$ + $\frac{3}{16}$ = $\frac{5}{16}$ This fraction cannot be further simplified.4) $\frac{1}{18}$ + $\frac{1}{6}$ = ?
$\frac{1}{18}$ + $\frac{3}{18}$ = $\frac{4}{18}$ = $\frac{2}{9}$
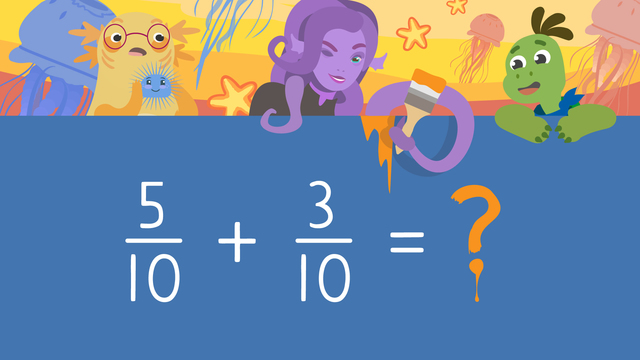
Adding Fractions
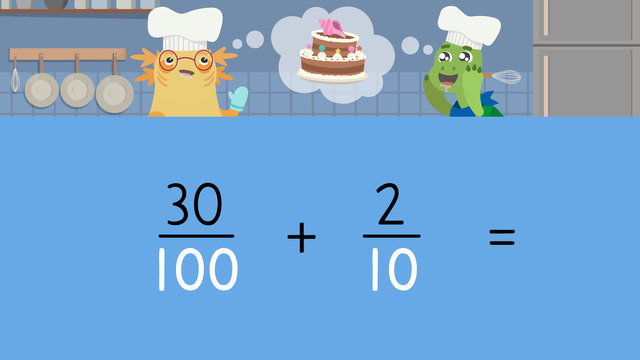
Adding Tenth and Hundredth

Adding Tenth and Hundredth — Let's Practise!
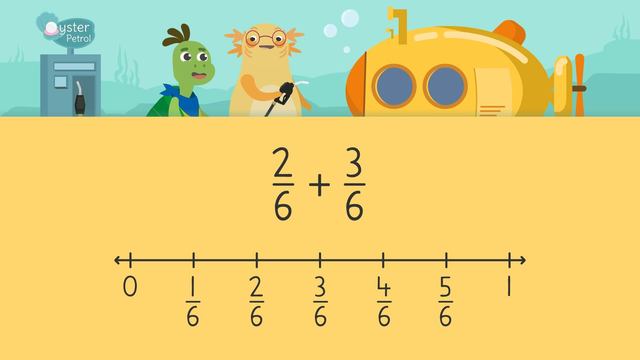
Adding Fractions on a Number Line
Adding Fractions on a Number Line- Let's Practise!
Subtracting Fractions on a Number Line
Subtracting Fractions on a Number Line — Let's Practise
Adding and Subtracting Mixed Numbers

Adding and Subtracting Mixed Numbers with Common Denominators—Let's Practise!

Adding Fractions with Different Denominators
Adding Mixed Numbers with Unlike Denominators


 Do you want to learn faster and more easily?
Do you want to learn faster and more easily?









