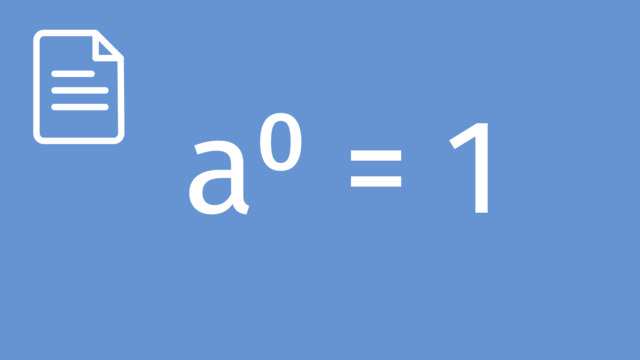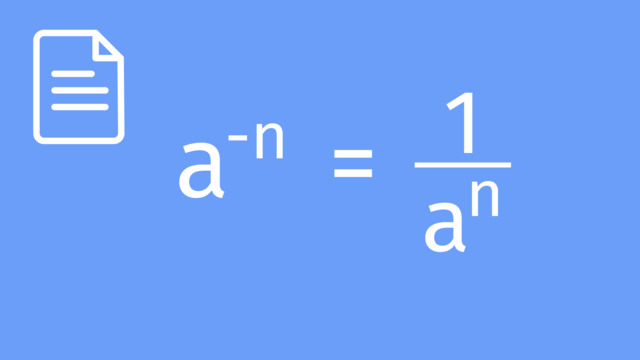The Definition of Negative Exponents
Do you want to learn faster and more easily?
Learning text on the topic The Definition of Negative Exponents
Negative Exponents – Introduction
Negative exponents are an essential concept in algebra, often encountered in scientific notation, algebraic expressions, and real-world scenarios such as calculating decay rates or understanding exponential growth in finance. A negative exponent indicates repeated division, contrary to a positive exponent, which denotes repeated multiplication. Keep in mind that exponents, also known as indices, represent the same mathematical concept.
A negative exponent expresses how many times the reciprocal of the base is multiplied by itself. For instance, $a^{-n}$ means $1$ divided by $a$ multiplied by itself $n$ times.
Negative Exponents – Explanation
The shift from positive to negative exponents represents a transition from multiplication to division in terms of how we handle the base number. With positive exponents, like $a^{3}$, we multiply the base ($a$) by itself a certain number of times (three times here). However, with negative exponents, such as $a^{-3}$, it indicates division. Instead of multiplying the base, we divide $1$ by the base multiple times. This reflects the inverse relationship - while positive exponents grow the number, negative exponents reduce it reciprocally.
Example:
- Positive Exponent: $2^{3} = 2 \times 2 \times 2 = 8$
- Negative Exponent: $2^{-3} = \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} = \frac{1}{8}$
Practice converting negative exponents to positive exponents.
The Laws of Exponents
To understand the definition of negative exponents, it is important to understand the proofs of laws of indices. Here, you will see all the important laws of exponents, including the law of negative exponents!
| Law | Mathematical Representation | Description |
|---|---|---|
| Product of Powers | $a^{m} \times a^{n} = a^{m+n}$ | When multiplying like bases, add the exponents. |
| Quotient of Powers | $\frac{a^{m}}{a^{n}} = a^{m-n}$ | When dividing like bases, subtract the exponents. |
| Power of a Power | $(a^{m})^{n} = a^{mn}$ | When raising a power to a power, multiply the exponents. |
| Zero Exponent | $a^{0} = 1$ (where $a \neq 0$) | Any non-zero number raised to the power of zero is one. |
| Negative Exponent | $a^{-n} = \frac{1}{a^{n}}$ | A negative exponent indicates the reciprocal of the base raised to the positive exponent. |
Let’s practise applying these laws of exponents and specifically involving negative exponents.
Product of Powers: Simplify $2^{-3} \times 2^{-2}$.
- Add the exponents: $2^{-3} \times 2^{-2} = 2^{(-3)+(-2)} = 2^{-5}$.
- Convert to a positive reciprocal: $2^{-5} = \frac{1}{2^{5}} = \frac{1}{32}$.
Quotient of Powers: Simplify $\frac{3^{-4}}{3^{-2}}$.
- Subtract the exponents: $\frac{3^{-4}}{3^{-2}} = 3^{-4-(-2)} = 3^{-2}$.
- Convert to a positive reciprocal: $3^{-2} = \frac{1}{3^{2}} = \frac{1}{9}$.
Power of a Power: Simplify $(5^{-2})^{3}$.
- Multiply the exponents: $(5^{-2})^{3} = 5^{-2 \times 3} = 5^{-6}$.
- Convert to a positive reciprocal: $5^{-6} = \frac{1}{5^{6}}$.
Try some on your own!
Understanding Negative Exponents with Expansion
Expanding an expression written in exponential notation can help us better visualise how negative exponents work.
Expand and simplify the expression: $\frac{5^{3}}{5^{7}}$
Expand Both Exponents:
- Numerator $5^{3}$ as $5 \times 5 \times 5$
- Denominator $5^{7}$ as $5 \times 5 \times 5 \times 5 \times 5 \times 5 \times 5$
Divide Step by Step:
- Each $5$ in the numerator cancels out a $5$ in the denominator.
- Left with $\frac{1}{5 \times 5 \times 5 \times 5}$ (four $5$'s remain in the denominator).
Result After Cancellation: $\frac{1}{5^{4}}$. This can also be written as $5^{-4}$.
Practise some expanding and working with negative exponents on your own
Negative Exponents – Summary
Key Learnings from this Text:
- Negative exponents represent reciprocal values and repeated division.
- Understanding and applying exponent rules is crucial for simplifying expressions.
- Expanding negative exponents helps to understand their meaning visually.
- Converting negative exponents to positive exponents simplifies the expression.
Definition of Negative Exponents – Frequently Asked Questions
