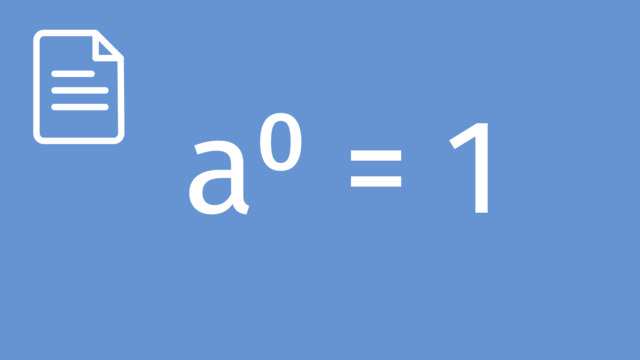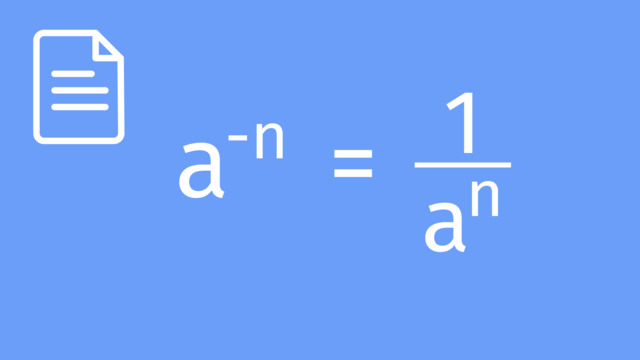Magnitude
- Understanding Magnitude through Powers of Ten – Introduction
- Understanding Magnitude – Definition
- Magnitude and Powers of Ten – Example
- Magnitude and Powers of Ten – Guided Practice
- Magnitude and Powers of Ten – Exercises
- Understanding Magnitude through Powers of Ten – Summary
- Understanding Magnitude through Powers of Ten – Frequently Asked Questions
Learning text on the topic Magnitude
Understanding Magnitude through Powers of Ten – Introduction
When we look at the world around us, we see a vast range of sizes, from the microscopic to the astronomical. Grasping the sheer scale of different objects can be challenging without a way to measure and compare them. This is where the concept of magnitude and the use of powers of ten come in handy, especially when learning about scientific notation.
Understanding Magnitude – Definition
Magnitude refers to the size or extent of something, often measured in terms of its power or scale. In mathematics, we frequently use powers of 10 to represent and compare the magnitude of very large or very small quantities. A power of ten is 10 raised to an index (exponent), which indicates how many times to multiply 10 by itself.
To make sense of magnitude, let's look at some rules and steps:
| Concept | Description |
|---|---|
| Powers of Ten | Written as $10^{n}$, where $n$ is the index. Large numbers have positive $n$, small numbers have negative $n$. |
| Scientific Notation | A method to express numbers as a product of a number between 1 and 10 and a power of ten, e.g., 320 as $3.2 \times 10^{2}$. |
| Comparing Magnitudes | To compare two numbers in scientific notation, check their indices; the larger index indicates a greater magnitude. |
Magnitude and Powers of Ten – Example
Let's take David's curiosity about the size difference between himself and Hans the ant as an example. David is 167.45 centimetres tall, which can be approximated to $1.67 \times 10^{2}$ centimetres in scientific notation. The ant, being 0.32 centimetres long, is approximately $3.2 \times 10^{-1}$ centimetres.
To find out how many times larger David is than Hans, we compare the powers of ten:
$ \frac{1.67 \times 10^{2}}{3.2 \times 10^{-1}} $
Here, we do not need the exact numbers but instead focus on the indices:
$10^{2} \div 10^{-1} = 10^{2 - (-1)} = 10^{3} $
So, David is about $10^{3}$, or 1,000 times larger than Hans.
Magnitude and Powers of Ten – Guided Practice
Imagine you're comparing the height of a basketball player, who is 2 metres tall, to the length of a basketball, which is about 24 centimetres in diameter.
Magnitude and Powers of Ten – Exercises
Now, let's apply what we've learned to a new scenario.
Understanding Magnitude through Powers of Ten – Summary
Key Learnings from this Text:
- Powers of ten help us estimate and compare the size of various entities.
- Scientific notation is a valuable tool for expressing very large or very small numbers.
- By comparing indices, we can easily determine how many times larger or smaller one quantity is than another.
- Understanding the magnitude and powers of ten is essential for real-world applications and scientific understanding.
Explore more about powers of ten and their applications with interactive practice problems, engaging videos, and printable worksheets on our platform to enhance your learning experience.
 Do you want to learn faster and more easily?
Do you want to learn faster and more easily?