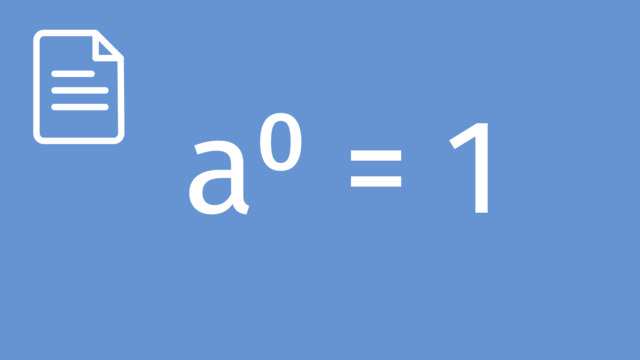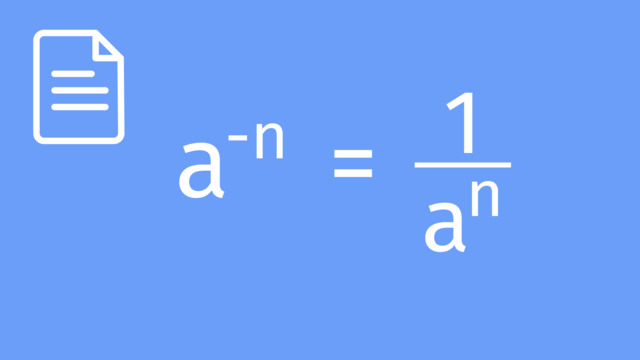Proofs of Laws of Indices
Do you want to learn faster and more easily?
Learning text on the topic Proofs of Laws of Indices
Proofs of Laws of Indices
In algebra, numbers written in index notation are used to represent repeated multiplication of the same number. Understanding and proving the laws of indices is essential in mathematics, as they frequently appear in various calculations, from simple algebraic expressions to complex scientific formulas.
The laws of indices are rules that describe how to handle exponential expressions, especially when multiplying, dividing or raising powers to other powers.
Understanding Proofs of Laws of Indices – Explanation
The laws of indices include several rules, each crucial for simplifying and solving exponential expressions.
Product of Powers
Product of Powers: When multiplying powers with the same base, add the indices.
Proof: Consider $a^{m} \times a^{n}$. Expanding this, we get $a \times a \times ...$ ($m$ times) multiplied by $a \times a \times ...$ ($n$ times). The total count of '$a$'s being multiplied is $m + n$, proving that $a^{m} \times a^{n} = a^{m+n}$.
| Example | Solution |
|---|---|
| Simplify $4^{3} \times 4^{2}$ | $4^{5}$ |
| Simplify $5^{2} \times 5^{3}$ | $5^{5}$ |
| Simplify $2^{4} \times 2^{2}$ | $2^{6}$ |
Division of Powers
Division of Powers: When dividing powers with the same base, subtract the index of the denominator from the index of the numerator. This concept is also fundamental to understanding division with indices.
Proof: Consider $\dfrac{a^{m}}{a^{n}}$. Expanding, we get $\dfrac{a \times a \times ... (m \text{times})}{a \times a \times ... (n \text{times})}$. Cancelling out the common '$a$'s, we're left with $m-n$ of them, so $\dfrac{a^{m}}{a^{n}} = a^{m-n}$.
| Example | Solution |
|---|---|
| Simplify $\dfrac{5^{7}}{5^{2}}$ | $5^{5}$ |
| Simplify $\dfrac{10^{6}}{10^{3}}$ | $10^{3}$ |
| Simplify $\dfrac{3^{8}}{3^{5}}$ | $3^{3}$ |
Power of a Power
Power of a Power: When raising a power to another power, multiply the indices. This principle not only applies to the powers of products and quotients but also to numbers in exponential form raised to a power.
Proof: Consider $(a^{m})^{n}$. Expanding the inner power, we have $a^{m} \times a^{m} \times ...$ ($n$ times). Each $a^{m}$ has '$m$' occurrences of '$a$', so in total, we have $m \times n$ occurrences, thus $(a^{m})^{n} = a^{mn}$.
| Example | Solution |
|---|---|
| Simplify $(3^{2})^{3}$ | $3^{6}$ |
| Simplify $(4^{3})^{2}$ | $4^{6}$ |
| Simplify $(2^{5})^{4}$ | $2^{20}$ |
Power of Zero
Power of Zero: Any base raised to the power of zero equals one. This concept is closely related to Numbers Raised to the Zeroth Power.
Proof: Consider $a^{m} \div a^{m} = a^{m-m}$. According to the quotient rule, this equals $a^{0}$. Since $a^{m} \div a^{m} = 1$, it proves $a^{0} = 1$.
| Example | Solution |
|---|---|
| Evaluate $6^{0}$ | $1$ |
| Evaluate $4^{0}$ | $1$ |
| Evaluate $(-5)^{0}$ | $1$ |
These examples illustrate the Power of Zero law, which asserts that any number raised to the power of zero equals one.
Negative Indices
Negative Indices: A negative index indicates the reciprocal of the base raised to the positive exponent. This principle is an essential part of understanding zero and negative indices**.
Proof: Consider $a^{-n}$. This can be written as $\dfrac{1}{a^{n}}$. Therefore, the negative index signifies an inverse relationship.
| Example | Solution |
|---|---|
| Evaluate $3^{-2}$ | $\dfrac{1}{3^{2}} = \dfrac{1}{9}$ |
| Evaluate $2^{-3}$ | $\dfrac{1}{2^{3}} = \dfrac{1}{8}$ |
| Evaluate $5^{-1}$ | $\dfrac{1}{5^{1}} = \dfrac{1}{5}$ |
Proofs of Laws of Indices – Practice
Laws of Indices
| Law | Expression | Result |
|---|---|---|
| Product of Powers | $a^{m} \times a^{n}$ | $a^{m+n}$ |
| Division of Powers | $\dfrac{a^{m}}{a^{n}}$ | $a^{m-n}$ |
| Power of a Power | $(a^{m})^{n}$ | $a^{mn}$ |
| Power of Zero | $a^{0}$ | $1$ |
| Negative Indices | $a^{-n}$ | $\dfrac{1}{a^{n}}$ |
Refer to the table for a recap, and practise applying the laws of indices.
Proofs of Laws of Indices – Summary
Key Learnings from this Text:
- Understanding and proving the laws of indices solidifies the foundation in algebra and higher-level mathematics.
- Each law, whether it's the Product of Powers or Division of Powers, simplifies complex exponential expressions.
- Applying these rules to variables and numerical bases demonstrates their universal applicability.
- The proofs of these laws lie in their ability to systematically expand and simplify exponential expressions.
For more, have a look at standard and scientific notation, using operations with scientific notation and multiplication with indices.
Proofs of Laws of Indices– Frequently Asked Questions
Proofs of Laws of Indices exercise
-
What is the meaning of the key words?
HintsAn example of the product:
the product of $4\times5 = 20$.
An example of the quotient:
the quotient of $\frac{20}{4} = 5$.
A fraction has a numerator and a denominator.
Solution- The value above the line of a fraction $=$ Numerator.
- The value below the line of a fraction $=$ Denominator.
- A result obtained by dividing one quantity by another $=$ Quotient.
- The result of multiplying two or more numbers together $=$ Product.
-
Use the product rule for indices.
HintsThe product rule for indices says that if the base is the same, we add the powers.
For example, $2^3\times2^4 = 2^{3+4} = 2^7$
When adding powers, remember that anything to the power $1$ does not have a power written.
For example, $6 = 6^1$, $3 = 3^1$
Solution- $4^3\times4^2 = 4^{2+3} = 4^5$
- $4^2\times4^2 = 4^{2+2} = 4^4$
- $4^5\times4^2 = 4^{5+2} = 4^7$
- $4\times4^2 = 4^{1+2} = 4^3$
-
Identify the laws of indices.
HintsAn example of the product of powers rule is, $x^4 \times x^3 = x^7$.
We add the powers when the base is the same.
An example of the division of powers rule is, $x^8 \div x^3 = x^5$.
We subtract the powers when the base is the same.
An example of the power of powers rule is, $(x^4)^6 = x^{24}$.
We could write this as, $x^4 \times x^4 \times x^4 \times x^4 \times x^4 \times x^4$.
In short, multiply the powers $x^{4\times6} = x^{24}$.
There are $4$ correct answers here.
SolutionThere are $4$ correct answers:
- $x^{a} \times x^{b} = x^{a+b}$
- $x^{a} \div x^{b} = x^{a-b}$
- $(x^{a})^{b} = x^{ab}$
- $y^{c} \times y^{d} = y^{c+d}$
-
Manipulate the indices.
Hints- We start this by stating that $a$ and $b$ are greater than $0$.
- Next, we are manipulating the left side to look like the right side.
- We expand the $y$'s to the power of $a$ for the next line.
- We then show there are $b$ lots of $y^a$.
- Finally, we show this shortens to the right side.
SolutionHere we can see the steps in the correct order.
-
Use the power of powers rule.
HintsWe use the power of power rule.
Multiply the indices if the base is the same.
For example, $(x^5)^3 = x^{5\times3} = x^{15}$.
To show this rule, we could write this out in full and use the product of powers rule.
For example,
$(x^5)^3 = x^{5} \times x^{5} \times x^{5} = x^{5+5+5} = x^{15}$
Solution$(x^2)^4 = x^{2} \times x^{2} \times x^{2} \times x^{2} = x^{2+2+2+2} = x^{8}$.
In short, $x^{2\times4}$ $ = x^8$.
-
Prove the power of powers law.
HintsWe use all the laws of indices for this proof. Here is one example.
Another example of the laws used.
There are $3$ laws used in this proof, therefore $3$ correct answers.
SolutionThe $3$ laws used are:
- Law of Negative Indices.
- Power of a Quotient Law.
- Power of Powers Law.
