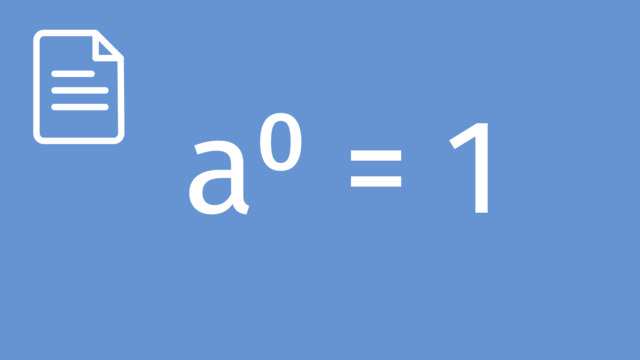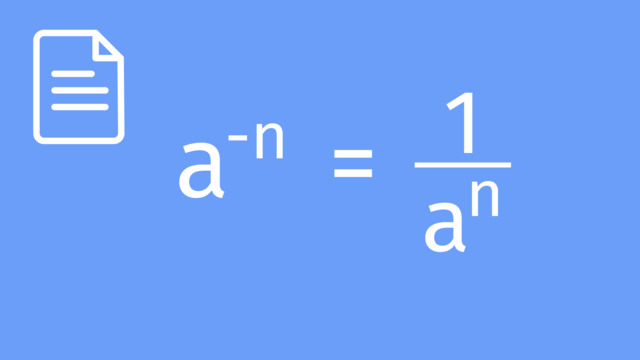Numbers Raised to the Zeroth Power
Do you want to learn faster and more easily?
Learning text on the topic Numbers Raised to the Zeroth Power
Numbers Raised to the Zeroth Power – Definition
Understanding the power of zero is an essential part of learning algebra. This concept is a piece of the broader puzzle of the laws of indices, which are vital for simplifying expressions and solving equations involving exponential notation. Keep in mind that powers, also known as exponents and indices, represent the same mathematical concept.
The power of zero may seem simple, but it plays a significant role in mathematical computations and has real-world applications in areas like computer science and engineering. By learning how numbers behave when raised to the power of zero, you're unlocking an important skill in mathematics.
The Power of Zero Rule states that any non-zero number raised to the power of zero equals one. In simpler terms, no matter what number you start with, if you raise it to the power of zero, the result is always one.
Numbers Raised to the Zeroth Power – Explanation
To truly grasp why anything raised to the power of zero is one, it's essential to understand the concept of exponents. Exponents indicate how many times a number, known as the base, is multiplied by itself. The power of zero is a unique case in this system.
Let’s take a look at some examples of problems involving a zeroth power.
Simplify: $\frac{m^{4}}{m^{4}}$
- Divide with same base: When we have the same base in both the numerator and the denominator, we subtract the exponents.
- Expansion: $\frac{m^{4}}{m^{4}} = m^{4-4}$
- Simplification: $m^{4-4} = m^{0}$
- Solution: $m^{0} = 1$
Simplify: $(m^{-3})(m^{3})$
- Multiply with same base: When we multiply powers with the same base, we add their exponents.
- Expansion: $(m^{-3})(m^{3}) = m^{-3+3}$
- Simplification: $m^{-3+3} = m^{0}$
- Solution: $m^{0} = 1$
Simplify: $\frac{5^{n}}{5^{n}}$ for any positive integer $n$
- General form: This represents a general case where any positive integer $n$ is the exponent.
- Divide with same base: Similar to the first problem, we subtract the exponents when dividing like bases.
- Solution: $\frac{5^{n}}{5^{n}} = 5^{n-n} = 5^{0} = 1$
Practise some own your own!
Numbers Raised to the Zeroth Power – Application
Evaluate $4^{x} \div 4^{x}$ when $x = 5$
- Substitute the value of $x$: Replace $x$ with 5 in the expression.
- Calculation: $4^{5} \div 4^{5}$
- Simplify: As the bases are the same, we subtract the exponents.
- Expansion: $4^{5-5} = 4^{0}$
- Solution: $4^{0} = 1$
Evaluate $(2^{x-1}) \times (2^{1-x})$ when $x = 3$
- Substitute the value of $x$: Replace $x$ with 3.
- Calculation: $(2^{3-1}) \times (2^{1-3})$
- Simplify: Add the exponents since the bases are the same.
- Expansion: $2^{2} \times 2^{-2} = 2^{2-2} = 2^{0}$
- Solution: $2^{0} = 1$
Evaluate $\frac{(5^{x})(5^{2x})}{5^{3x}}$ when $x = 2$
- Substitute the value of $x$: Replace $x$ with 2.
- Calculation: $\frac{(5^{2})(5^{4})}{5^{6}}$
- Simplify: Add exponents in the numerator and subtract from the exponent in the denominator.
- Expansion: $\frac{5^{6}}{5^{6}} = 5^{6-6} = 5^{0}$
- Solution: $5^{0} = 1$
Try some on your own!
Numbers Raised to the Zeroth Power – Summary
Key Learnings from this Text:
- Understanding the power of zero is crucial in algebra and simplifying expressions.
- The Power of Zero Rule, stating any non-zero number raised to the power of zero equals one, is a key concept in exponents.
- This rule is not just theoretical; it has practical applications in fields like computer science and engineering.
- Mastering this concept aids in developing a stronger grasp of mathematical principles and problem-solving techniques.
Understanding the proofs of laws of indices helps simplify and solve problems with ease.
Numbers Raised to the Zeroth Power – Frequently Asked Questions
