Multiplying Mixed Numbers: Word Problems
- Multiplying Mixed Numbers – Word Problems
- Mixed Numbers and Improper Fractions
- Conversion between Mixed Numbers and Improper Fractions
- Multiplying Mixed Numbers: Word Problems – Step-by-Step Process
- Multiplying Mixed Numbers: Word Problems – Practice
- Multiplying Mixed Numbers: Word Problems – Summary
- Multiplying Mixed Numbers: Word Problems – Frequently Asked Questions
Learning text on the topic Multiplying Mixed Numbers: Word Problems
Multiplying Mixed Numbers – Word Problems
Understanding how to work with mixed numbers is essential in our daily lives. From cooking recipes to measuring materials for a project, we often encounter situations where mixed numbers come into play. Gaining comfort in multiplying these numbers helps in effectively solving real-world problems.
Mixed Numbers and Improper Fractions
It's really helpful to know about improper fractions and mixed numbers when you're solving maths problems, so let's make sure we understand what they are!
Mixed Number: A number consisting of a whole number and a fraction, like 2½.
Improper Fraction: A fraction where the numerator (top number) is greater than or equal to the denominator (bottom number), such as $\frac{7}{4}$.
Conversion between Mixed Numbers and Improper Fractions
| Process | Description | Example |
|---|---|---|
| Mixed to Improper Conversion | Multiply the whole number by the denominator, add the numerator, then place over the denominator. | $2 \frac{1}{2}$ → $\frac{2 \times 2 + 1}{2}$ = $\frac{5}{2}$ |
| Improper to Mixed Conversion | Divide the numerator by the denominator. The quotient is the whole number, the remainder over the denominator is the fraction. | $\frac{7}{4}$ → $1 \frac{3}{4}$ |
Convert the mixed number $3 \frac{1}{4}$ to an improper fraction.
- Multiply the whole number part by the denominator and add the numerator.
- $3 \times 4 + 1 = 12 + 1 = 13$.
- The mixed number $3 \frac{1}{4}$ is equal to the improper fraction $\frac{13}{4}$.
Convert the improper fraction $\frac{11}{3}$ to a mixed number.
- Divide the numerator by the denominator.
- $11 \div 3 = 3$ remainder $2$.
- The improper fraction $\frac{11}{3}$ is equal to the mixed number $3 \frac{2}{3}$.
Multiplying Mixed Numbers: Word Problems – Step-by-Step Process
Multiplying a fraction by a whole number and dealing with two mixed numbers are common in real-world problems. It's important to understand how these calculations work in practical situations. Let’s practise some examples!
A recipe needs $1 \frac{2}{3}$ cups of sugar for a batch of cookies, and you want to make $2 \frac{1}{2}$ batches.
- Convert Mixed to Improper: Convert $1 \frac{2}{3}$ to $\frac{5}{3}$ and $2 \frac{1}{2}$ to $\frac{5}{2}$.
- Multiply: Multiply $\frac{5}{3}$ by $\frac{5}{2}$.
- Calculate & Convert Back: $\frac{5}{3} \times \frac{5}{2} = \frac{25}{6}$. Convert $\frac{25}{6}$ to a mixed number: $4 \frac{1}{6}$. You need $4 \frac{1}{6}$ cups of sugar.
If a garden requires $2 \frac{1}{4}$ cubic metres of soil for each section, and you are landscaping $3$ sections, how much soil is needed in total?
- Convert Mixed to Improper: Convert $2 \frac{1}{4}$ to an improper fraction: $\frac{2 \times 4 + 1}{4} = \frac{9}{4}$.
- Multiply: Multiply by 3: $\frac{9}{4} \times 3$.
- Calculate & Convert Back: $\frac{27}{4} = 6 \frac{3}{4}$. You need $6 \frac{3}{4}$ cubic metres of soil.
Each shelf needs $2 \frac{1}{2}$ feet of wood, and you are building $4$ shelves. How much wood in total?
- Convert Mixed to Improper: Convert $2 \frac{1}{2}$ to $\frac{5}{2}$.
- Multiply: Multiply by 4: $\frac{5}{2} \times 4$.
- Calculate & Convert Back: $\frac{20}{2} = 10$. You need $10$ feet of wood.
Multiplying Mixed Numbers: Word Problems – Practice
Practise some on your own!
Multiplying Mixed Numbers: Word Problems – Summary
Key Learnings from this Text:
- Multiplying mixed numbers is a practical skill for real-world applications.
- Conversion between mixed and improper fractions is key in multiplying mixed numbers.
- Multiplying mixed numbers involves converting to improper fractions, multiplying, and converting back.
- Understanding these steps helps in efficiently solving problems involving measurements, recipes, etc.
Multiplying Mixed Numbers: Word Problems – Frequently Asked Questions
Multiplying Mixed Numbers: Word Problems exercise
-
Barry needs $3 \frac{3}{4}$ metres of wood to build one section of a fence.
HintsConvert the mixed number $3 \frac{3}{4}$ into an improper fraction by multiplying the whole number by the denominator of the fraction part and then adding the numerator.
Multiply the resulting improper fraction by the number of sections to find the total amount of wood needed.
Solution1.) First, we convert $3 \frac{3}{4}$ to an improper fraction.
2.) Convert $3 \frac{3}{4}$ to an improper fraction:
$3 \times 4 + 3 = 15 \rightarrow \frac{15}{4}$
3.) Multiply the improper fraction by the number of sections:
$\frac{15}{4} \times 4 = \frac{60}{4} = 15$
4.) We now have the correct answer of $15$ metres.
-
Julia is hosting a pizza party and each guest eats $2 \frac{1}{2}$ slices of pizza.
HintsConvert $2 \frac{1}{2}$ to an improper fraction:
$2 \times 2 + 1 = 5 \rightarrow \frac{5}{2}$
Multiply the improper fraction by the number of guests:
$\frac{5}{2} \times 5 = \frac{25}{2}$
Convert $\frac{25}{2}$ back to a mixed number.
SolutionThey eat $12 \frac{1}{2}$ slices of pizza.
-
How much paint is used?
HintsConvert the mixed number $1 \frac{3}{5}$ into an improper fraction by multiplying the whole number part by the denominator of the fractional part and then adding the numerator.
Multiply the resulting improper fraction by the number of students to find out the total number of tubes needed for the class, and then convert the answer to a mixed number if necessary.
Solution$12\mathbf{\frac{4}{5}}$ tubes of paint are used by all the students.
1. Convert $1 \frac{3}{5}$ to an improper fraction: $1 \times 5 + 3 = 8 \rightarrow \frac{8}{5}$
2. $\frac{8}{5} \times 8 = \frac{64}{5} = 12 \frac{4}{5}$
-
How many seed packets are used?
HintsConvert both mixed numbers into improper fractions.
Multiply the numerators and multiply the denominators.
Convert this answer back to a mixed number.
SolutionSandy will use $7\frac{1}{2}$ packets of seeds.
Convert $3\frac{1}{3}$ to an improper fraction - $\frac{10}{3}$
Convert $2\frac{1}{4}$ to an improper fraction - $\frac{9}{4}$
Multiply $\frac{10}{3} \times \frac{9}{4} = \frac{90}{12}$
Convert $\frac{90}{12}$ to a mixed number - $7\frac{6}{12}$ which is simplified to $7\frac{1}{2}$.
-
A recipe calls for $1 \frac{1}{3}$ cups of sugar to make a batch of cookies.
HintsConvert $1 \frac{1}{3}$ to an improper fraction by multiplying $1 \times 3$ and adding $1$.
When multiplying the improper fraction by a whole number, multiply the numerator only.
SolutionThe total amount of sugar needed to make 3 batches of cookies is 4 cups.
1.) $1 \frac{1}{3}$ = $\frac{4}{3}$
2.) $\frac{4}{3} \times 3 =$ $\frac{12}{3}$
3.) $\frac{12}{3}$ = $4$
4.) The total amount of sugar needed to make $3$ batches of cookies is $4$ cups.
-
Solve the multiplication problems.
HintsConvert the mixed numbers to improper fractions before multiplying.
When multiplying a fraction by a single number, just multiply the numerator.
When multiplying two fractions, multiply the numerators and multiply the denominators.
Solution$3\frac{1}{10} \times 3 = 9\frac{3}{10}$
$4\frac{1}{2} \times 2\frac{1}{6} = 9\frac{3}{4}$
$5\frac{2}{3} \times 2 = 11\frac{1}{3}$
$1\frac{3}{4} \times 3\frac{1}{4} = 5\frac{11}{16}$

Fractions as a Multiple of Unit Fractions
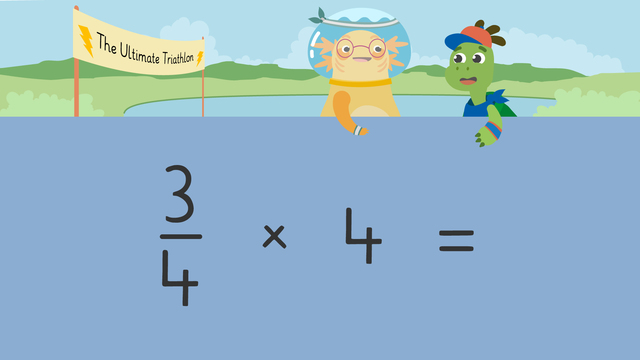
Multiplying a Fraction by a Whole Number

Multiplying Fractions Less Than One
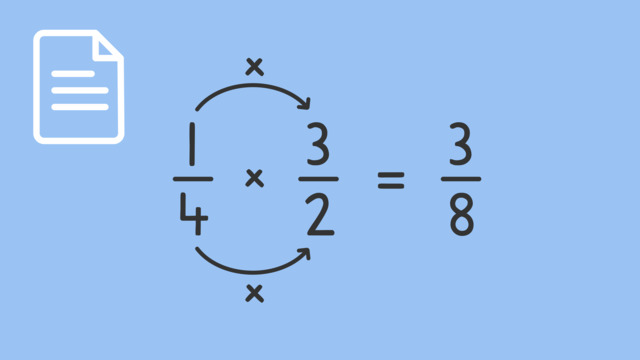
Multiplying Fractions
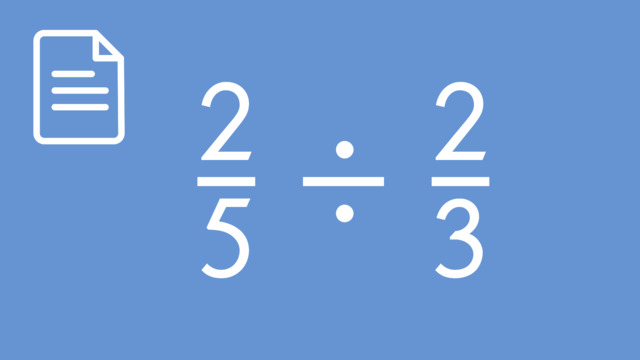
Dividing Fractions
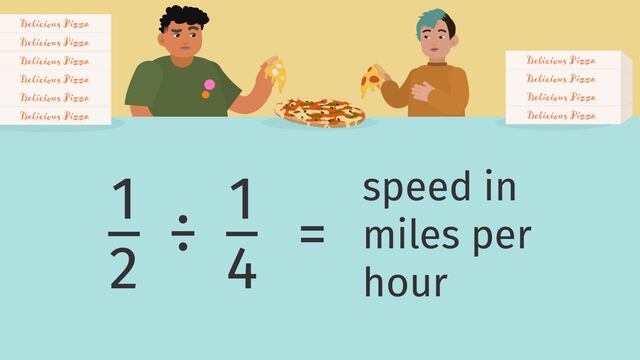
Ratios of Fractions

Dividing Whole Numbers by Unit Fractions Using Models

Lowest Common Multiples

Multiplying Mixed Numbers: Word Problems

Finding the Greatest Common Factor
 Do you want to learn faster and more easily?
Do you want to learn faster and more easily?













