Finding the Greatest Common Factor


Basics on the topic Finding the Greatest Common Factor
Finding the Greatest Common Factor – Introduction
In mathematics, the concept of finding the greatest common factor (GCF) is incredibly useful for solving a variety of problems. Whether simplifying fractions, solving equations, or analyzing ratios, understanding how to determine the GCF can simplify computations and lead to more elegant solutions. Let's dive into what the greatest common factor is and how to find it.
Understanding the Greatest Common Factor – Definition
The greatest common factor (GCF), sometimes known as the greatest common divisor (GCD) or highest common factor (HCF), is the largest whole number that is a divisor of two or more given numbers.
The GCF is instrumental in simplifying fractions, solving problems with ratios, and even in everyday situations like dividing a set of items into equal groups without leftovers.
How to Find the GCF – Method
There are several methods to find the GCF, including prime factorisation and listing. Let's look at one method, prime factorisation.
Steps to Find the GCF:
- Decompose each number into prime factors.
- Identify the common prime factors.
- Multiply these common prime factors together to get the GCF.
For instance, to find the GCF of 18 and 24:
- Prime factors of 18: 2 × 3 × 3
- Prime factors of 24: 2 × 2 × 2 × 3
- Common factors are 2 and 3
- Thus, GCF(18, 24) = 2 × 3 = 6
Check your understanding so far.
Finding the Greatest Common Factor – Guided Practice
Suppose we want to find the GCF of 45 and 75. Follow the steps of prime factorisation:
- List the prime factors for both numbers.
- Circle the common prime factors.
- Multiply these to calculate the GCF.
Let’s find the GCF of 45 and 75.
Try practising finding the GCF on your own!
Finding the Greatest Common Factor – Summary
Key Learnings from this Text:
- The greatest common factor is the highest number that divides two or more numbers without leaving a remainder.
- Prime factorisation is a reliable method to find the GCF.
- The GCF is useful in simplifying fractions, distributing goods evenly, and more.
Explore other content on our website platform for interactive practice problems, videos, and printable worksheets that support your educational journey in understanding factors and multiples.
Finding the Greatest Common Factor – Frequently Asked Questions
Transcript Finding the Greatest Common Factor
Luis and June seem to be struggling to find some common factors between them. Speaking of common factors, let's learn about finding the greatest common factor. The greatest common factor, or
Finding the Greatest Common Factor exercise
-
What is GCF?
HintsWhen finding the GCF, we are looking for something that two or more numbers share or have in common.
The GCF of 12 and 15 is 3. This is the biggest number that fits equally into 12 and 15.
SolutionGCF stands for Greatest Common Factor.
It is the largest number that divides equally into two or more numbers.
-
Find the GCF of 12 and 24.
HintsAll of the factors of 12 are also factors of 24, which is the greatest?
Greatest means the largest common factor.
SolutionThe Greatest Common Factor (GCF) of 12 and 24 is 12.
This is the largest number that equally divides into both numbers.
-
Find the GCF of 54 and 72.
HintsFill in the gaps in each factor tree first.
How many times does 27 go into 54? This is a factor pair.
Once you have completed each factor tree, look for the shared factors.
You should find the shared factors of 2, 3 and 3. Multiply these together to find the GCF.
SolutionThe greatest common factor of 54 and 72 is 18.
When we complete the factor trees for 54 and 72, we can find the shared factors of 2, 3 and 3. When we multiply 2 $\times$ 3 $\times$ 3 we get 18.
-
Can you find the GCF of these pairs of numbers?
HintsDraw out factor pairs for smaller numbers or factor trees for larger numbers.
For 15 and 30, draw factor pairs. Here is one for 15, can you draw one for 30 and then find the GCF?
For 126 and 154, factor trees would be helpful.
Once you have drawn your factor trees, look for all of the shared factors and multiply them to find the GCF.
Solution- The GCF of 15 and 30 is 15.
- The GCF of 84 and 144 is 12.
- The GCF of 126 and 154 is 14.
- The GCF of 21 and 35 is 7.
-
Find the GCF of 12 and 18.
HintsFirst look for common factors. Which numbers are factors of both 12 and 18?
Out of these common factors, which one is the greatest or largest number?
SolutionThe correct answer is 6.
The common factors are: 1, 2, 3 and 6.
Out of these common factors, 6 is the greatest.
-
Can you solve the problem?
HintsYou need to find the greatest common factor of 72, 96 and 104.
Draw a factor tree for each of these numbers and look for the shared factors.
You should find the shared factors of 2, 2 and 2. Multiply these together to find the answer.
SolutionThe greatest number of bunches is 8.
The greatest common factor of 72, 96 and 108 is 8, therefore, this is the greatest number of bunches Cara can make with the same number of of each colour of balloon.

Fractions as a Multiple of Unit Fractions
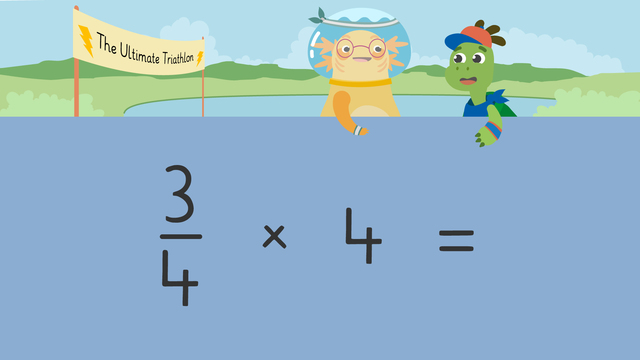
Multiplying a Fraction by a Whole Number

Multiplying Fractions Less Than One
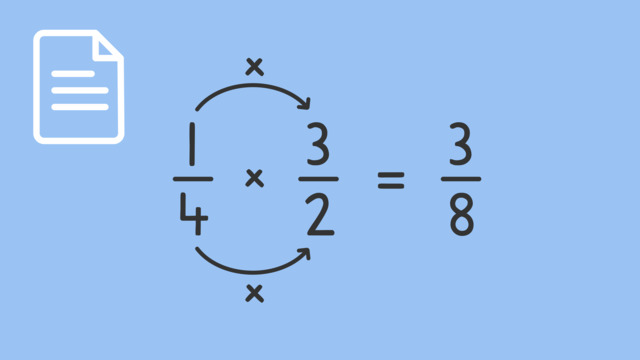
Multiplying Fractions
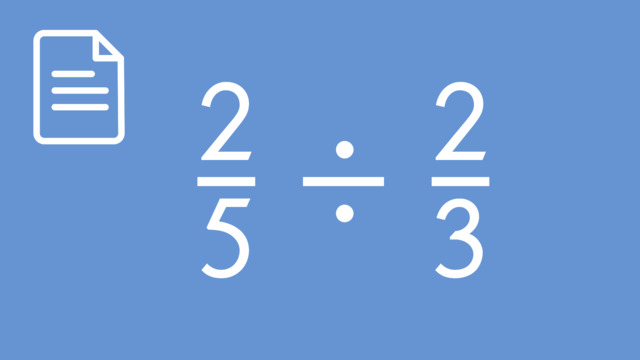
Dividing Fractions
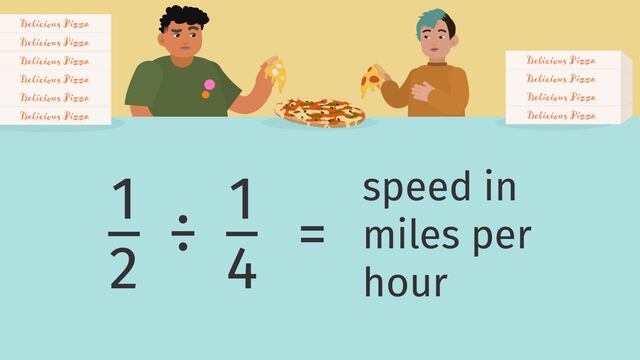
Ratios of Fractions

Dividing Whole Numbers by Unit Fractions Using Models

Lowest Common Multiples

Multiplying Mixed Numbers: Word Problems

Finding the Greatest Common Factor
 Do you want to learn faster and more easily?
Do you want to learn faster and more easily?









