Dividing Whole Numbers by Unit Fractions Using Models


Basics on the topic Dividing Whole Numbers by Unit Fractions Using Models
Learn how to divide whole numbers by unit fractions using models.
Transcript Dividing Whole Numbers by Unit Fractions Using Models
Ah, breakfast. A time for breaking the overnight fast and satisfying our hunger! But first, let's satisfy your hunger for knowledge and learn about dividing whole numbers by unit fractions using models. You may already know that division is a process of sharing or splitting a number into equal parts, and that a unit fraction is a fraction where the numerator is one. But what happens when you divide whole numbers by unit fractions? Let's say we have one whole pancake and we want to divide this into quarters. The division sentence for this would be one divided by one quarter. We are simply asking how many quarters are there in this whole pancake? This circle represents our pancake. The complete circle is one whole. Since the division sentence asks us to divide the whole by one-quarter, we can split the model into equally sized quarters. Then, to find the answer, we simply count how many quarter pieces there are in this whole. There are four one quarter pieces in this whole, so one divided by one-quarter is four. It is important to remember that anytime you divide a whole number by a unit fraction, your quotient will always be a value greater than the whole number you began with. Now it's your turn! This time, there are three muffins and each one needs to be divided into thirds. Pause the video to solve the problem and press play when you are ready for the solution. First, set up a model for the muffins; we need three whole circles. Then, divide each muffin into thirds, like this. Finally, count all the one third pieces there are in all three muffins. There are nine one third pieces of muffins, so three divided by one third is nine. Now for the final problem! There are four pieces of bacon, which will be divided into one fifth pieces. Pause the video to solve the problem and press play when you are ready for the solution. First, set up a model for the bacon; this time we will use four fraction bars. Then divide each piece into fifths. Finally, count all the one fifth pieces there are in all four pieces of bacon. Four divided by one fifth is twenty. To summarise, when dividing whole numbers by unit fractions, remember you are asking how many of the unit fractions make up the whole. As a result, the quotient will always be a whole number greater than the one you began with. Hopefully todays learning has given you some food for thought!
Dividing Whole Numbers by Unit Fractions Using Models exercise
-
What does each keyword mean?
HintsA fraction contains a numerator and a denominator. Which is the top and which is the bottom?
Examples of unit fractions are
$\frac{1}{3} , \frac{1}{5} , \frac {1}{2} , \frac{1}{10}$
What do you notice about these?
A cake is split into six equal slices. The splitting is called division and the individual slices are fractions of the cake.
SolutionA fraction is a part of a whole.
A numerator is the top number in a fraction.
A denominator is the bottom number in a fraction.
Division is sharing or splitting a number into equal parts.
A unit fraction is a fraction where the numerator is one.
-
How many quarters are there in three chocolate bars?
HintsThe model should represent the question. First, check how many chocolate bars are in the question.
Next, check how many pieces each bar is cut into. The denominator of the unit fraction tells you this.
Finally, count the number of pieces in total.
SolutionHere we can see the correct answer.
There are three chocolate bars split into quarters (four pieces). Counting the pieces gives 12 pieces, therefore, the answer is $3 \div \frac{1}{4} = 12$.
-
Dividing a whole number by a unit fraction.
HintsThe first number tells us how many items there are.
The denominator of the unit fraction tells us how many parts the item is split into.
Two cakes split into four equal slices would be represented by the math sentence $2 \div \frac{1}{4} = 8$
SolutionThe image shows the correct solutions.
Sweets: $3 \div \frac{1}{4} = 12$
Chocolate bars: $2 \div \frac{1}{6} = 12$
Pizza: $4 \div \frac{1}{3} = 12$
Muffins: $6 \div \frac{1}{2} = 12$
-
Divide the whole numbers by the unit fraction.
HintsWhen dividing a whole number by a unit fraction, we are counting how many times the fraction is in the whole.
When dividing a whole number by a unit fraction, the quotient will always be a number greater than the whole number you started with.
If you have five pizzas and divide each pizza in half, how many slices would you have?
SolutionIn the image we can see the first solution:
$\bf{5 \div \frac{1}{2} = 10}$ because there are $2$ equal pieces in each of the $5$ wholes.
--------------------------------------------------------------------------------------------
$\bf{4 \div \frac{1}{4} = 16}$ because there are $4$ equal pieces in each of the $4$ wholes.
$\bf{9 \div \frac{1}{3} = 27}$ because there are $3$ equal pieces in each of the $9$ wholes.
$\bf{6 \div \frac{1}{3} = 18}$ because there are $3$ equal pieces in each of the $6$ wholes.
-
How many quarters are there in two cakes?
HintsEach cake is represented by one whole. There are two whole cakes.
The denominator tells us how many equal pieces the cakes are split into. In the image we can see that each cake has been split into four equal pieces.
Another way to read the question is - the two cakes are divided into quarters, how many pieces are there?
Look at the image for a similar question. There are $3$ muffins, the whole number is written first. It is divided into thirds, the fraction is written after the division sign.
SolutionThe correct maths sentence is $2 \div \frac{1}{4}$ because there are two cakes each divided into quarters.
There are $\bf{8}$ quarters in the two cakes.
-
Five cakes are cut into thirds. How many slices are there?
HintsThere are five cakes, this is your whole number.
Each cake is split into equal slices. The denominator of the unit fraction tells you how many equal slices.
Each cake has three equal slices.
SolutionYou have five cakes, each one is split into thirds.
This means that each of the five cakes is split into three slices. There are $\bf{15}$ slices in total.
$5 \div \frac{1}{3} = 15$

Fractions as a Multiple of Unit Fractions
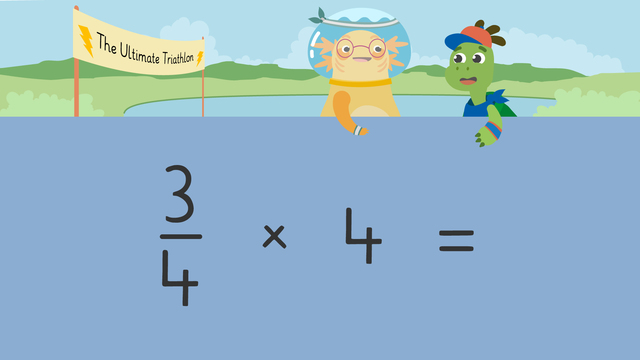
Multiplying a Fraction by a Whole Number

Multiplying Fractions Less Than One
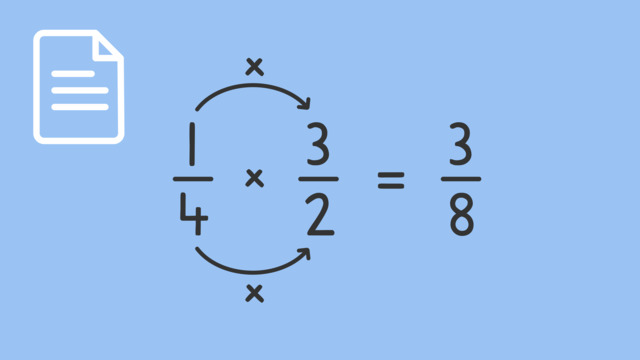
Multiplying Fractions
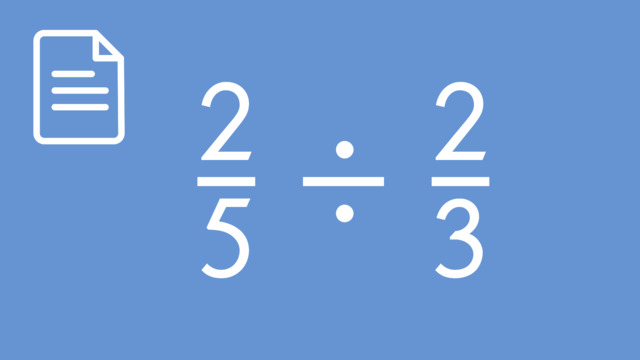
Dividing Fractions
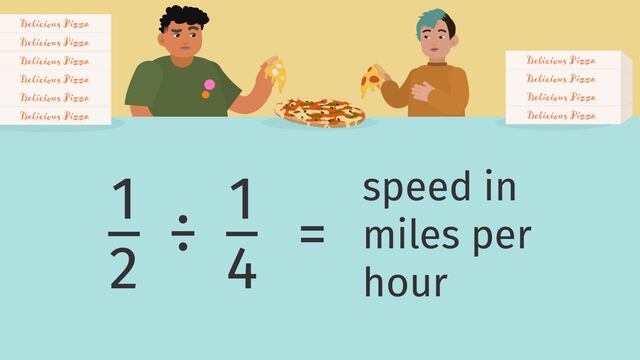
Ratios of Fractions

Dividing Whole Numbers by Unit Fractions Using Models

Lowest Common Multiples

Multiplying Mixed Numbers: Word Problems

Finding the Greatest Common Factor


 Do you want to learn faster and more easily?
Do you want to learn faster and more easily?









