Lowest Common Multiples

Basics on the topic Lowest Common Multiples
Lowest Common Multiples – Introduction
Calculating the Lowest Common Multiple (LCM) is a fundamental skill in mathematics that can simplify many types of problems, particularly those involving fractions, ratios, or periodic events. It is the basis for finding common denominators in fractions and plays a crucial role in arithmetic and algebra.
Lowest Common Multiples – Definition
The Lowest Common Multiple of two or more numbers is the smallest positive integer that is divisible by each of the numbers without any remainder.
It's a concept that is frequently used to solve problems involving fractions, addition, subtraction and to find equivalent fractions. Let's explore how LCM is used and why it's such an important concept in maths.
Lowest Common Multiples – Uses
Using the LCM allows us to find the smallest shared multiple between numbers, which facilitates operations such as adding and comparing fractions. It's also used when we want to synchronize events that happen in cycles, like traffic lights or scheduling.
How to Find Lowest Common Multiples – Example
The process of finding the LCM can be done in several ways, including listing the multiples, using prime factorisation, or employing the greatest common divisor (GCD). Here's an example using the listing method:
Lowest Common Multiples – Application
LCMs have various real-world applications. They are particularly useful in situations where different cycles need to be synchronized, such as in scheduling, baking, or planning events.
Least Common Multiples – Summary
Key Learnings from this Text:
- LCM is the smallest number into which two or more given numbers can evenly divide.
- It is crucial for adding, subtracting, and comparing fractions with different denominators.
- Understanding LCMs can simplify various real-world problems and facilitate synchronization.
- While calculating LCMs, one can use the listing method, prime factorisation, or the GCD approach.
Consider exploring more about LCMs and their applications in other areas of mathematics such as finding equivalent fractions and Solving Problems with Equivalent Ratios.
Lowest Common Multiples – Frequently Asked Questions
Transcript Lowest Common Multiples
In a world where nature's symphony turns sinister, they thought they knew the rhythm of the cicadas. But when two ancient broods converge, they'll face a swarm like never before! By learning about lowest common multiples, we can determine when they will next strike together! There are times you will need to apply more than one multiple to a situation or problem, like determining when two different broods of periodical cicadas will emerge at the same time. To do this, you would need to find their lowest common multiple. This is the smallest number that can be divided by both numbers without a remainder. There are two methods for finding the

Fractions as a Multiple of Unit Fractions
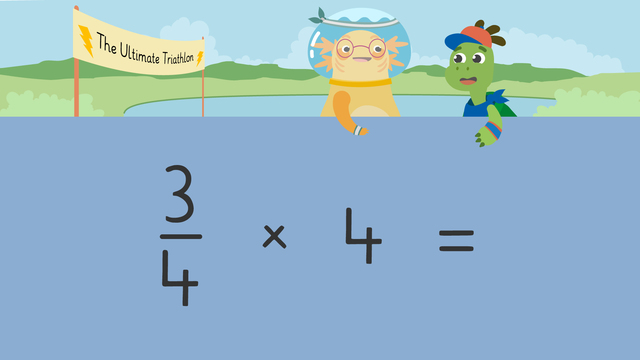
Multiplying a Fraction by a Whole Number

Multiplying Fractions Less Than One
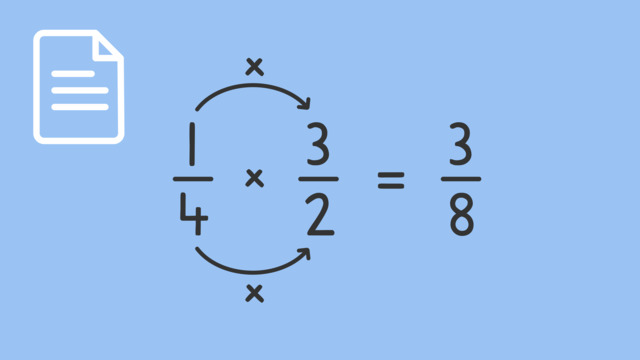
Multiplying Fractions
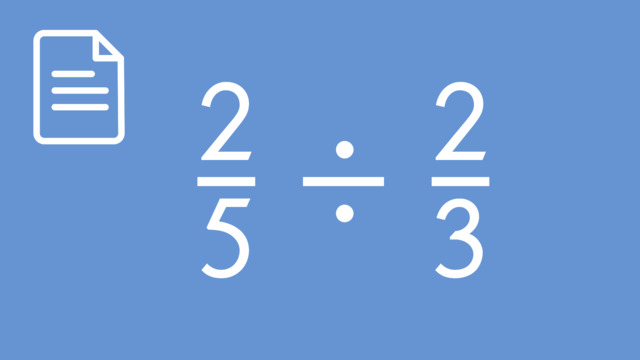
Dividing Fractions
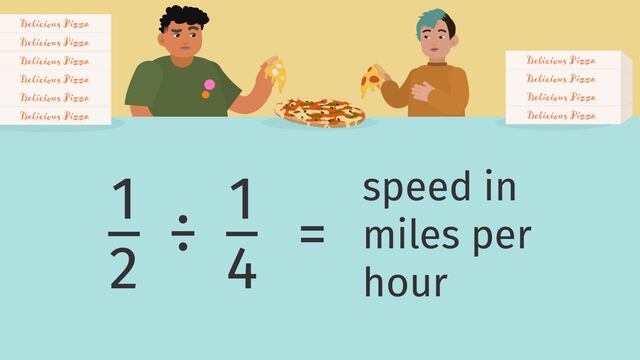
Ratios of Fractions

Dividing Whole Numbers by Unit Fractions Using Models

Lowest Common Multiples

Multiplying Mixed Numbers: Word Problems

Finding the Greatest Common Factor
 Do you want to learn faster and more easily?
Do you want to learn faster and more easily?






