Understanding and Applying Pythagoras' Theorum
Learning text on the topic Understanding and Applying Pythagoras' Theorum
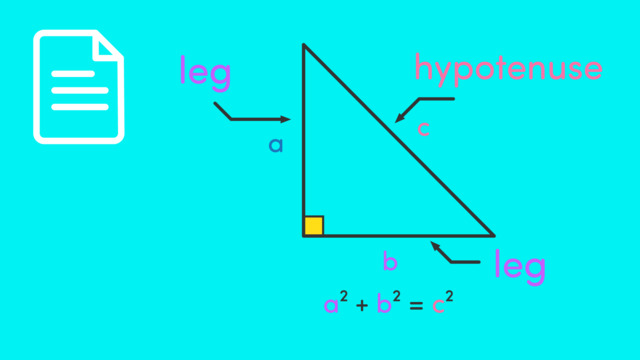
What is Pythagoras’ Theorem?
Pythagoras’ theorem is a practical and essential concept in geometry, widely used in numerous real-world scenarios. From determining the shortest path in navigation to calculating the height of a building or the length of a ramp, this theorem is a fundamental tool. It's not just a mathematical formula; it's a practical solution for various everyday problems involving right angled triangles.
Understanding Pythagoras’ Theorem
Pythagoras’ Theorem states that in a right angled triangle, the square of the hypotenuse (the side opposite the right angle) equals the sum of the squares of the other two sides, known as the legs. The theorem is typically written as $a$$^2$ + $b$$^2$ = $c$$^2$ where the $c$ is the hypotenuse, or the longest side, and the $a$ and $b$ are the legs of the triangle.
The Pythagorean equation specifically works for a right angled triangle, but to learn more about other triangles, check out this video: Different Types of Triangles
Brief History
The theorem is named after the Greek mathematician Pythagoras, who popularised it, though it was known in various cultures before his time.
Real-World Examples
Pythagoras’ theorem is widely used in the real world. Here we provide some examples from the fields of architecture, navigation and technology:
| Application Area | Use of Pythagoras’ Theorem |
|---|---|
| Architecture and Construction | Calculating the height of a structure or the length of a supporting beam. |
| Navigation | Determining the shortest path between two points. |
| Technology | Designing components in various fields of engineering. |
Using the Theorem – Step-by-Step Examples
Identify the Right Angled Triangle: First, ensure you're working with a right angled triangle (one angle is 90 degrees).
Label the Sides: Label the longest side (opposite the right angle) as $c$ (the hypotenuse). The other two sides are labelled $a$ and $b$ and are called the legs.
Apply the Formula: Use $a$$^2$ + $b$$^2$ = $c$$^2$ to find the missing side. If you know $c$ and one leg, solve the formula to find the other leg. Solve the equation for the missing variable.
Let’s go through this exercise together!
If a ladder is placed against a wall and reaches $15$ feet high, and the base is $9$ feet away from the wall, how long is the ladder?
- Firstly, label your hypotenuse $c$, and the legs $a$ and $b$.
- Next, substitute the known values into the theorem $9$$^2$ + $15$$^2$ = $c$$^2$.
- Then, calculate: 81 + 225 = $c$$^2$.
- Finally, solve for $c$: $c = \sqrt{306} \approx 17.5$ feet to 1 decimal place.
Let’s complete one more exercise together.
A rectangular park measures 80 metres by 60 metres. Find the length of the diagonal path across the park.
Notice this rectangle is made up of two right angled triangles if we draw a diagonal line connecting one corner to the other. These right angled triangles are identical but just flipped.
- First, label your sides $a$, $b$ and $c$.
- Next, substitute the known values into the theorem: $80$$^2$ + $60$$^2$ = $c$$^2$.
- Then, calculate: 6400 + 3600 = $c$$^2$.
- Finally, solve for $c$: $c = \sqrt{6400 + 3600} = \sqrt{10000} = 100$ metres.
Pythagoras’ Theorem – Exercises with Solutions
Pythagoras’ Theorem – Summary
- At its core, Pythagoras’ theorem provides a mathematical method to determine the relationship between all three sides of any right angled triangle.
- Pythagoras’ Theorem, crucial for calculations in right angled triangles, asserts that $a$$^2$ + $b$$^2$ = $c$$^2$, where $c$ is the hypotenuse and $a$ and $b$ are the other two sides.
- Applied in diverse real-world situations such as architecture, navigation and technology, this theorem helps calculate distances and structural dimensions.
- To solve for an unknown side, square the lengths of the known sides, add or subtract these values, and take the square root of the result to find the missing measurement.
- Pythagorean triples, like $(3, 4, 5)$ or $(5, 12, 13)$, provide quick reference solutions for some commonly encountered right angled triangles.
Discover more about geometry with our interactive practice problems, videos and worksheets on our platform!
Frequently Asked Questions – Pythagoras’ Theorem
Understanding and Applying Pythagoras' Theorum exercise
-
Find Pythagoras' Theorem.
HintsThe area of the square formed by the hypotenuse of a right triangle is equal to the sum of the areas of the squares formed by the triangle's other two sides.
The square of the hypotenuse (the longest side) of a right triangle is equal to the sum of the squares of the triangle's other two sides. For instance, consider a triangle with sides measuring $3$ cm, $4$ cm, and $5$ cm.
The calculation would be:
$3^2 + 4^2 = 5^2$
$9 + 16 = 25$
Solution$a^2 + b^2 = c^2$
Pythagoras' Theorem states that the square off the hypotenuse is equal to the squares off the other two sides added together.
We use $a$, $b$ and $c$ for short!
-
Find the missing length.
HintsTo find the hypotenuse we use Pythagoras' Theorem. Hypotenuse squared = shorter sides squared and added together.
$a^2 + b^2 = c^2$
Example
$h^2 = (3 \times 3) + (4 \times 4)$
$h^2 = 9 + 16$
$h^2 = 25$
$\sqrt{(h^2)} = \sqrt{25}$
$h = 5$cm
SolutionSides $3$ cm and $4$ cm have hypotenuse $5$ cm.
We used Pythagoras' Theorem.
$h^2 = (3 \times 3) + (4 \times 4)$
$h^2 = 9 + 16$
$h^2 = 25$
$\sqrt{(h^2)} = \sqrt{25}$
$h = 5$ cm
Sides $5$ cm and $12$ cm have hypotenuse $13$ cm.
$h^2 = (5 \times 5) + (12 \times 12)$
$h^2 = 25 + 144$
$h^2 = 169$
$\sqrt{(h^2)} = \sqrt{169}$
$h = 13$ cm
Sides $12$ cm and $16$ cm have hypotenuse $20$ cm.
$h^2 = (12 \times 12) + (16 \times 16)$
$h^2 = 144 + 256$
$h^2 = 400$
$\sqrt{(h^2)} = \sqrt{400}$
$h = 20$ cm
Sides $9$ cm and $12$ cm have hypotenuse $15$ cm.
$h^2 = (9 \times 9) + (12 \times 12)$
$h^2 = 81 + 144$
$h^2 = 225$
$\sqrt{(h^2)} = \sqrt{225}$
$h = 15$ cm
-
Help Molly find the missing length.
HintsUsing Pythagoras' Theorem, find the shorter side, $a$ this time. (Shown in dark green with the arrow)
$a^2 + b^2 = c^2$
You will need to rearrange this to make $a$ the subject.
$a^2 = c^2 - b^2$
$a^2 + b^2 = c^2$
Substitute the lengths into the formula.
$a^2 + 3^2 = 3.5^2$
We need to find $a$ so subtract $3^2$ from both sides.
$a^2 = 3.5^2 - 3^2$
Solution$\bf{1.8}$ metres
$a^2 + b^2 = c^2$
Substitute the lengths into the formula.
$a^2 + 3^2 = 3.5^2$
We need to find $a$, so subtract $3^2$ from both sides.
$a^2 = 3.5^2 - 3^2$
$a^2 = 12.25 - 9$
$a^2 = 3.25$
$\sqrt{(a^2)} = \sqrt{3.25}$
$a = 1.80277...$
We round to $1$ decimal place = $1.8$ metres
-
What is the distance from A to B?
HintsJoin the points and drop a right angled triangle off the diagonal. You can now use Pythagoras' Theorem.
$(AB)^2 = 7^2 + 5^2$
SolutionA to B = $8.6$ units to $1$ decimal place.
Join points A to B
Drop a right angled triangle.
Count the units of the base and the height.
Use Pythagoras' Theorem to find the hypotenuse.
$(AB)^2 = 7^2 + 5^2$
$(AB)^2 = 49 + 25$
$\sqrt{(AB)^2} = \sqrt{74}$
$AB - 8.6$ units to $1$ decimal place.
-
What is the missing length?
HintsPythagoras' Theorem states $6^2 + 8^2 = h^2$
or we can write it
$8^2 + 6^2 = h^2$
$a$ and $b$ can be changed but $c$, the hypotenuse is always on its own.
$h^2 = 6^2 + 8^2$
$h^2 = 36 + 64$
Continue to find $h$.
SolutionHypotenuse = $10$cm
$h^2 = 6^2 + 8^2$
$h^2 = 36 + 64$
$h^2 = 100$
$\sqrt{(h^2)} = \sqrt{100}$
$h = 10$cm
-
Apply the Pythagorean Theorem to find a perimeter.
HintsTo find the length of fencing we need the perimeter of the pen.
All the lengths are given except the hypotenuse.
Use Pythagoras' Theorem to find that first.
Using Pythagoras' Theorem on the triangle of height $5$ metres and base $7$ m - $4$ m = $3$ metres.
$c^2 = 5^2 + 3^2$
Complete this to find the hypotenuse.
When you have the hypotenuse:
$c^2 = 5^2 + 3^2$
$c^2 = 25 + 9$
$c^2 = 34$
$\sqrt{(c^2)} = \sqrt{34}$
$c = 5.8$ metres
Add this to the other lengths to get the perimeter.
Perimeter = all the sides added together.
Perimeter = $4 + 5 + 7 + 5.8$
SolutionFence should be $21.8$ metres long
Using Pythagoras' Theorem to find the missing hypotenuse first.
A height of $5$ m and base of $7$ m - $4$ m = $3$ m
$c^2 = 5^2 + 3^2$
$c^2 = 25 + 9$
$c^2 = 34$
$c = 5.8$ to $1$ decimal place
Fencing needed: $7 + 5 + 5.8 + 4 = 21.8$ metres
 Do you want to learn faster and more easily?
Do you want to learn faster and more easily?