The Converse of the Pythagorean Theorem
- The Converse of the Pythagorean Theorem
- The Converse of the Pythagorean Theorem – Explanation
- The Converse of the Pythagorean Theorem – Examples
- The Converse of the Pythagorean Theorem – Practice
- The Converse of the Pythagorean Theorem – Summary
- The Converse of the Pythagorean Theorem – Frequently Asked Questions
Learning text on the topic The Converse of the Pythagorean Theorem
The Converse of the Pythagorean Theorem
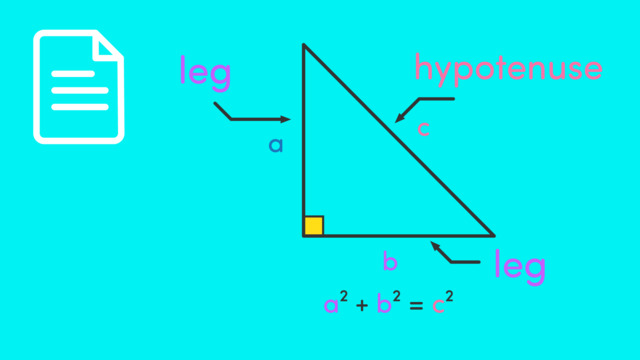
The converse of the Pythagorean Theorem is an important idea in geometry. It helps us figure out if a triangle has a right angle. If adding the squares of the two shorter sides equals the square of the longest side, then the triangle is a right triangle. Applying the Pythagorean Theorem is very useful for solving maths problems and is also used in many real-life situations where right angles are needed.
The Converse of the Pythagorean Theorem states that for any triangle with sides of lengths a, b, and c (where c is the longest side), if a2 + b2 = c2 holds true, then the triangle is a right triangle with the right angle opposite side c.
The Converse of the Pythagorean Theorem – Explanation
The converse of the Pythagorean Theorem helps confirm the nature of a triangle by relating the squares of its side lengths. This property is especially useful in fields like construction, where confirming right angles is crucial for the integrity of structures.
| Step | Description | Detail |
|---|---|---|
| 1 | Identify the sides | Determine which side would be the hypotenuse if the triangle were right-angled. This is always the longest side, $c$. |
| 2 | Apply the theorem | Square the lengths of the shorter sides ($a$ and $b$) and sum them up. |
| 3 | Compare the sum to $c^{2}$ | If $a^{2} + b^{2}$ equals $c^{2}$, the triangle is right. |
The Converse of the Pythagorean Theorem – Examples
Let’s practise some together.
Example 1: Triangle with sides 6 units, 8 units, and 10 units
- Identify the sides: The longest side, which would be the hypotenuse in a right triangle, is $c = 10$ units.
- Apply the theorem: Calculate and sum the squares of the other two sides: $a^{2} = 6^{2} = 36$ and $b^{2} = 8^{2} = 64$. The sum is $a^{2} + b^{2} = 36 + 64 = 100$.
- Compare the sum to $c^{2}$: Since $c^{2} = 10^{2} = 100$ and $a^{2} + b^{2} = c^{2}$, by the converse of the Pythagorean Theorem, the triangle is a right triangle.
Example 2: Triangle with sides 5 units, 6 units, and 11 units
- Identify the sides: The longest side, which would be the hypotenuse in a right triangle, is $c = 11$ units.
- Apply the theorem: Calculate and sum the squares of the other two sides: $a^{2} = 5^{2} = 25$ and $b^{2} = 6^{2} = 36$. The sum is $a^{2} + b^{2} = 25 + 36 = 61$.
- Compare the sum to $c^{2}$: Since $c^{2} = 11^{2} = 121$ and $a^{2} + b^{2} $\neq$ c^{2}$, by the converse of the Pythagorean Theorem, the triangle is not a right triangle.
Let’s apply the converse of the Pythagorean Theorem to determine if a triangle with sides of 5 units, 12 units, and 13 units is a right triangle.
Is the triangle with sides measuring 9 units, 12 units, and the longest side (hypotenuse) measuring 15 units a right triangle? Let’s apply the converse of the Pythagorean Theorem!
Can a triangle with side lengths of 7 units, 24 units, and a hypotenuse of 25 units be classified as a right triangle? Use the Pythagorean Theorem to find out.
The Converse of the Pythagorean Theorem – Practice
The Converse of the Pythagorean Theorem – Summary
Key Learnings from this Text:
- The converse of the Pythagorean Theorem allows us to verify whether a triangle is a right triangle.
- By verifying that $a^{2} + b^{2} = c^{2}$, where $c$ is the longest side, we can conclusively determine the triangle's right-angle nature.
The Converse of the Pythagorean Theorem – Frequently Asked Questions
The Converse of the Pythagorean Theorem exercise
-
Find the square of the numbers.
HintsWhen we square a number we multiply it by itself. A skill we need when we are using the Pythagorean Theorem. For example, $4^2 = 4\times4 = 16$
When we square a decimal with one decimal place the answer will have two decimal places. For example, $0.1^2 = 0.1\times0.1 = 0.01$.
Solution- $3^2 = 3\times3 = 9$. We can see this above as the area of a square with sides $3$.
- $0.5^2 = 0.5\times0.5 = 0.25$
- $5^2 = 5\times5 = 25$
- $0.2^2 = 0.2\times0.2 = 0.04$
-
Understanding the converse of the Pythagorean theorem.
HintsWe use the Pythagorean Theorem to find out if the triangle is right angled.
If, $a^2 + b^2$ is the same value as $c^2$ then the triangle is right angled.
Substitute the values into the theorem and square them.
For example, to check this triangle we use:
- $a^2 + b^2 = c^2$
- $2^2 + 3^2 = 4^2$
- $4 + 9 = 16$
- This is not correct as $4 + 9 = 13$ not $16$ therefore, the triangle is not right angled.
Solution- The Pythagorean Theorem states that $a^2 + b^2 = c^2$
- Using this triangle $7^2 + 40^2 = 42^2$
- We square all of the numbers so, $49 + 1600 = 1764$. This sum is incorrect.
- Therefore the triangle is not right angled.
-
Use the converse of the Pythagorean Theorem.
HintsFor a triangle to be right angled, the Pythagorean Theorem should be true. That is $a^2 + b^2 = c^2$, where $c$ is the longest side, the hypotenuse.
For example, if $a = 9$, $b = 12$ and $c = 15$ we can use the Pythagorean theorem to check if the triangle is right angled.
- $a^2 + b^2 = c^2$
- $9^2 + 12^2 = 15^2$
- $81 + 144 = 225$
- As $81 + 144$ does $= 225$, the triangle is right angled.
There are $2$ correct answers.
SolutionRight angled triangles are:
- $a = 3, b = 4, c = 5$ as $3^2 + 4^2 = 5^2$ as $9 + 16 = 25$ : Correct
- $a = 6, b = 8, c = 10$ as $6^2 + 8^2 = 10^2$ as $36 + 64 = 100$ : Correct.
- $a = 4, b = 5, c = 6$ as $4^2 + 5^2 = 6^2$ as $16 + 25 = 36$ : Not correct.
- $a = 8, b = 10, c = 12$ as $8^2 + 10^2 = 12^2$ as $64 + 100 = 144$ : Not correct.
-
Use the Pythaogrean theorem to prove which triangle has a right angle.
HintsFor a triangle to be right angled, the Pythagorean Theorem should be true. That is $a^2 + b^2 = c^2$, where $c$ is the longest side, the hypotenuse.
For example, if $a = 1$, $b = 2$ and $c = 3$ we can use the Pythagorean theorem to check if the triangle is right angled.
- $a^2 + b^2 = c^2$
- $1^2 + 2^2 = 3^2$
- $1 + 4 = 9$
- As $1 + 4$ does not $= 9$, the triangle is not right angled.
SolutionThe right angled triangle is:
- $a = 1.5, b = 2, c = 2.5$
- $1.5^2 + 2^2 = 2.5^2$
- $2.25 + 4 = 6.25$
_______________________________________________________
The others are not equal so are not right angled triangles.
For example,
- $a = 2, b = 4, c = 6$
- $2^2 + 4^2 = 6^2$
- $4 + 16 = 36$. This is not correct, so is not a right angled triangle.
-
Identifying the sides of a right triangle.
HintsThe Pythagorean Theorem states that the squares next to the two shorter sides added together are equal to the square next to the hypotenuse.
Pythagorean Theorem is $a^2 + b^2 = c^2$, where $c$ is the hypotenuse.
The hypotenuse is the side opposite the right angle, and is the longest side in a right angled triangle.
As an example, we can see here that,
- $3^2 + 4^2 = 5^2$
- $3^2 = 9$
- $4^2 = 16$
- $5^2 = 25$
- $9 + 16 = 25$
SolutionThe Pythagorean Theorem is $a^2 + b^2 = c^2$ where $c$ is the hypotenuse (the longest side, opposite the right angle).
-
Indirect proof
HintsWhen completing an indirect proof of a right triangle we firstly write the statement and assume the triangle is not a right angled triangle.
We use the triangle to try to prove it is NOT right angled. That means it is not equal to $a^2 + b^2 = c^2$.
If we find the assumption is not correct, we can say it is a right angled triangle.
SolutionAn indirect proof is when we state the theorem, then try to prove otherwise. If we cannot prove otherwise then we can indirectly say the theorem is correct.
 Do you want to learn faster and more easily?
Do you want to learn faster and more easily?