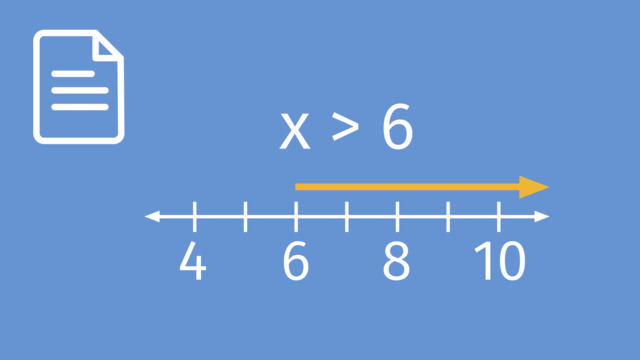Inequalities on a Number Line
Do you want to learn faster and more easily?
Learning text on the topic Inequalities on a Number Line
Inequalities on a Number Line – Definition
Inequalities on a number line allow us to visually interpret and solve expressions comparing different values. This concept is widely used in various fields such as mathematics, economics, and engineering, helping us understand scenarios like budget constraints, temperature ranges, or any situation where comparison between numbers is required.
An inequality on a number line represents a range of values that satisfy a certain condition. It involves symbols like $>$ (greater than), $<$ (less than), $\geq$ (greater than or equal to), and $\leq$ (less than or equal to).
Don’t forget that inequalities can be written in different ways but convey the same information. For example, $x > 2$ and $2 < x$ both show that $x$ is greater than 2, or that 2 is less than $x$.
Inequalities on a Number Line – Explanation
Inequalities are graphed on a number line to determine the set of numbers that satisfy the inequality. This is crucial for solving problems involving limits and ranges. The basic elements used in graphing include:
| Symbol | Description | Example |
|---|---|---|
| Open Circle | Indicates that the number is not part of the solution set. | $x > a$ or $x < a$ |
| Closed Circle | Indicates that the number is part of the solution set. | $x \geq a$ or $x \leq a$ |
| Arrow Direction | Points towards the range of numbers that make the inequality true. | Indicates the range of solutions. |
Inequalities on a Number Line – Example
Let’s practise by graphing the inequality $x \leq -2$ on a number line.
Step 1: Identify the Location
- Locate the position where $x = -2$ on the number line.
Step 2: Mark the Point
- Place a closed circle at -2 to indicate that -2 is included in the solution set.
Step 3: Determine the Arrow Direction
Decide which direction to draw the arrow. Since the inequality is $x \leq -2$, the arrow should:
- Point to the left to show that all numbers less than or equal to -2 are included.
Step 4: Describe the Solution Set
Explain the range of numbers that solve the inequality:
- The solution set includes all numbers less than or equal to -2, visually represented by a line extending from -2 to the left indefinitely.
Inequalities on a Number Line – Practice
Using some paper, practice graphing inequalities on number lines.
Inequalities on a Number Line – Summary
Key Learnings from this Text:
- Inequalities on a number line allow for visual comparison of numbers, commonly used in mathematics, economics, and engineering.
- An inequality on a number line shows a range of values meeting a specific condition using symbols like $>$, $<$, $\geq$, and $\leq$.
- Key elements in graphing include open circles (excluding the number) and closed circles (including the number), with arrows indicating the direction of the inequality.
- Practising graphing inequalities on a number line helps understand and solve problems involving ranges and limits of values.
For more, check out our learning text on solving inequalities.
Inequalities on a Number Line – Frequently Asked Questions
