What are fractions?
Do you want to learn faster and more easily?
Basics on the topic What are fractions?
What Are Fractions in Maths?
What are fractions used for? Fractions in maths are used to represent equal parts of a whole or equal parts of a group. Below are examples of equal parts of a whole and equal parts of a group.
Fractions – Overview
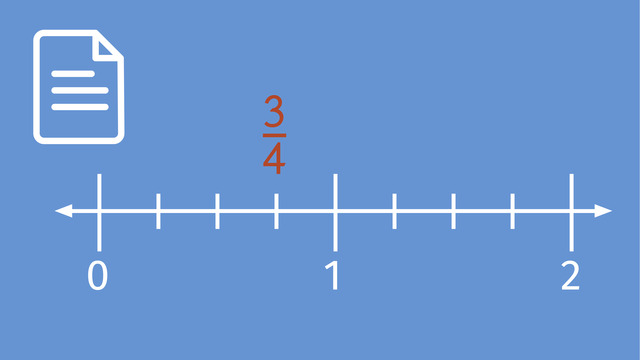
What are Two Big Ideas in the Learning of Fractions? The first big idea is that fractions are represented with a numerator, the top number, and the denominator, the bottom number. These are separated by a fraction bar.
The second big idea is that fractions represent an equal portion of a whole or a group. For example, they could represent one-half of a whole watermelon.
Another example is that fractions could also represent an equal part of a collection, or group, of cards.
Fractions – Summary
Fractions represent an equal part of a whole or group. They have a numerator, a denominator, with a fraction bar that separates them. Below you will find worksheets and practise problems to further develop your understanding of fractions.
| Term | Example |
|---|---|
| Numerator | 1 |
| Fraction bar | — |
| Denominator | 4 |
Frequently Asked Questions concerning Fractions
Transcript What are fractions?
Axel and Tank are getting ready for a games night! "Axel, look at this on our list, what's that?" "Oh, that Tank, is called a fraction!" Let's help answer Tank's question, "What are fractions?" You may have seen fractions before, like these! So, what exactly are fractions? Fractions are equal parts of a whole or a group! Fractions are used when we talk about parts of a whole or parts of a group! To show this, fractions are written in two parts. The top number, called the numerator, represents how many of the equal parts of the whole you have. The bottom number, called the denominator, represents how many equal parts are in the whole or whole group, in total. They are divided by a line called a fraction bar. For example, Axel and Tank's shopping list says they need one half of a watermelon for games night. In this situation, we are talking about a part of a WHOLE. The entire watermelon represents the whole. Axel and Tank want one half. So we need to divide the watermelon into two equal parts because the denominator tells us the whole has two parts. The numerator is one, so we take one of the two parts of watermelon! Now they have their one half of a watermelon. What about the other item they have bought? They need one-quarter of the twelve cards they bought to complete their set for games night. First, let's open the card packet and get all twelve cards out. Because there is more than one whole this time, they have to find a fraction of a group! This time, we would identify the denominator which is four. Then share all twelve cards into four equal groups like this. Each group ends up with three cards in it. Now look at the numerator, which asks for one part of the four groups. They take one of these groups which has three cards in it. One quarter of a packet of twelve cards is three cards! While Axel and Tank head home for games night, let's summarise! Remember, fractions represent equal parts of a whole or group. Fractions consist of a numerator and a denominator which are separated by a fraction bar. Fractions can represent parts of whole or they can represent parts of a group. "And with this card, I claim VICTORY!" "MWAHAHA!" "NOOO! You have defeated me!" "Oh well! Same time again next week?"
What are fractions? exercise
-
Help identify the shapes that show $\frac1 4$.
HintsFirst, work out the denominator - bottom number. How many parts are there?
To show $\frac1 4$ the shape needs to be divided into 4 equal parts.
Next, work out the numerator - top number. To find this you need to count the number of equal parts shaded.
To find $\frac1 4$ 1 part out of 4 needs to be shaded.
In this example there are 5 equal parts. So the denominator - bottom number is 5.
There is 1 part shaded. So our numerator - top number is 1.
1 out of 5 is shaded. $\frac1 5$
SolutionTo identify a $\frac1 4$ it needs to have 4 equal parts and 1 of the 4 needs to be shaded.
The circle and triangle show $\frac1 4$ shaded in because there are 4 equal parts and 1 part is shaded in.
-
How much cake has been eaten?
HintsFirst, count how many slices are missing from the cake.
This will give you the numerator - top number.
Count how many equal slices the cake has been split into.
This will give you the denominator - bottom number.
In this example we can see that this cake was split into 4 equal parts.
There are 3 slices missing. So $\frac3 4$ of this cake has been eaten.
SolutionWhen working out the denominator (bottom number), we count how many equal parts the cake had been split into.
When working out the numerator (top number), we count to see how many slices were missing.
-
Help Axel and Tank identify what fractions of the chocolate, pizza and pie are left.
HintsFirst, count how many equal parts it has been split into. This will give you the denominator - bottom number.
Next, count the amount of parts that are left. This will give you the numerator - top number.
In this example, we can see that there are 6 equal parts.
2 parts have been eaten, so there are 4 pieces left.
This gives us the fraction $\frac4 6$.
Solution$\frac1 4$ - 4 equal parts with 1 part highlighted or left over.
$\frac2 3$ - 3 equal parts with 2 parts highlighted or left over.
$\frac2 5$ - 5 equal parts with 2 parts highlighted or left over.
-
Can you help match the fractions and answers?
HintsTo help find the fractions of amounts, we can look at the denominator - bottom number. This will tell us how many equal groups the total number has been split into.
Look at the numerator - top number. This will tell you how many of those equal groups you need.
For example, if there are 9 counters and you need to find $\frac1 3$; you would split the 9 into 3 equal groups. 1 group = 3 and would represent $\frac1 3$. 2 groups = 6 and would represent $\frac2 3$.
In this example there are 12 sweets.
If we want to find $\frac1 3$, we need to divide the whole amount 12 by 3 - the denominator - bottom number. This tells us how many equal groups we need.
12 $\div$ 3 = 4
SolutionTo find fractions of amounts we look at the denominator. This will tell us how many equal groups to split the items/objects into.
The numerator tells us how many of the groups we need.
$\frac1 4$ = 5 . We look at the amount of cards which is 25. Then we divide 25 by the denominator (bottom number). This gives us 5.
$\frac1 5$ = 2 . We look at the total number of counters which is 10. We then divide 10 by the denominator (bottom number) which is 5. 10 divided by 5 = 2.
$\frac2 3$ = 4 . 6 cards divided by the denominator 3 gives us 2. We then multiply this by the numerator as we want 2 of the groups $\frac2 3$. 2 x 2 = 4.
$\frac1 2$ = 6 . 12 counters divided by the denominator 2 = 6
-
Can you work out which images show $\frac1 3$ shaded?
HintsThe denominator is 3. This means that we are looking for a shape that has 3 equal parts.
The numerator - top number, tells us how many of those parts are shaded.
In this example it is showing 3 out of 4 squares are shaded.
The image consists of a rectangle spilt into 4 equal parts. The 4 will be our denominator which is the bottom number.
3 parts have been shaded in. 3 will be our numerator which is the top number of a fraction.
SolutionFirst, we must count the equal parts the shape has been split into.
We are looking for a shape that has 3 equal parts.
Next, we must find a shape where 1 part of the 3 is shaded.
All the highlighted shapes in the above image show $\frac1 3$.
-
Can you help Axel and Tank work out what they have left?
HintsThe denominator - bottom number tells us how many equal parts the whole has been split into.
The numerator - top number tell us the number of parts it represents.
SolutionWhat fraction of the cake has been eaten? $\frac3 4$
What fraction of the cake is left? $\frac1 4$
There are 16 cards in total.
There are 4 blue cards, 4 pink cards and 8 green cards.
What fraction of cards are blue? $\frac1 4$
There are 10 counters in total. 5 out of 10 counters are yellow.
The fraction of yellow counters is $\frac1 2$.
I love fractions