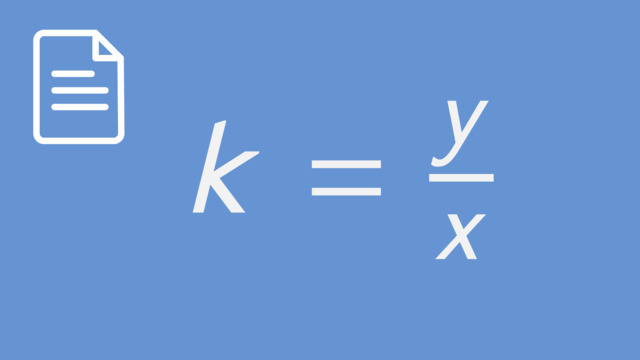Proportional Relationships and Measuring Rates
- Proportional Relationships and Measuring Rates
- Identifying Proportionality in Tables
- Writing Proportional Relationship Equations
- Applying Proportional Relationship Equations
- Proportional Relationships and Measuring Rates – Summary
- Proportional Relationships and Measuring Rates – Frequently Asked Questions
Learning text on the topic Proportional Relationships and Measuring Rates
Proportional Relationships and Measuring Rates
Proportional relationships are key to understanding how different quantities relate and influence each other. In maths, we explore these relationships to discover how consistently changing one thing can affect another. For instance, think about buying snacks at a movie theatre. If one bag of popcorn costs £3, then two bags would cost £6, three bags would cost £9, and so on. This consistent change - where the total cost changes in direct proportion to the number of popcorn bags - is a perfect example of a proportional relationship.
A proportional relationship is when two quantities increase or decrease at the same constant rate, meaning their ratio always remains the same. This consistent ratio shows how one quantity is directly related to the other.
| Concept | Explanation |
|---|---|
| Rate | A rate is a comparison of two different types of quantities, like speed (miles per hour) or density (people per square mile). |
| Ratio | A ratio shows how two quantities are related, like the ratio of cats to dogs in a pet store. |
| Unit Rate | The comparison of a quantity to one unit of another quantity, like if a car travels 60 miles in 2 hours, the unit rate is 30 miles per hour. |
| Constant of Proportionality ($k$) | This constant value shows the relationship between two quantities that are directly proportional to each other, calculated using the formula $k = \frac{y}{x}$. |
Identifying Proportionality in Tables
Finding rates with division is the key process for identifying proportional relationships in tables.
Checking for Proportional Relationships: Divide the '$y$' values by the corresponding '$x$' values. If these ratios are the same, then the relationship is proportional.
Finding the Constant of Proportionality: The consistent ratio value is the constant of proportionality.
Let’s look at some examples to find the proportionality in a table.
A car's fuel efficiency is measured over various distances. We have a table listing the distance travelled and the corresponding fuel used.
Checking for Proportional Relationships:
- For 50 miles: $\frac{2 \text{ litres}}{50 \text{ miles}} = \frac{2}{50}$
- For 100 miles: $\frac{4 \text{ litres}}{100 \text{ miles}} = \frac{4}{100}$
- For 150 miles: $\frac{6 \text{ litres}}{150 \text{ miles}} = \frac{6}{150}$
These ratios simplify to the same value: $\frac{1}{25}$.
Finding the Constant of Proportionality: Since all ratios are equal, the constant of proportionality is $\frac{1}{25}$ litres per mile.
A baker uses sugar in various batches of cookies. The table shows the relationship between the batches of cookies and the sugar used.
Check for Proportional Relationships:
- For 1 batch: $\frac{3 \text{ cups}}{1 \text{ batch}} = \frac{3}{1}$
- For 2 batches: $\frac{6 \text{ cups}}{2 \text{ batches}} = \frac{6}{2}$
- For 3 batches: $\frac{9 \text{ cups}}{3 \text{ batches}} = \frac{9}{3}$
These ratios simplify to the same value: $3$ cups per batch.
Finding the Constant of Proportionality: The constant of proportionality is $3$ cups per batch, as each ratio equals $3$.
Try some examples on your own!
Writing Proportional Relationship Equations
Representing proportional relationships with equations is key in maths. The equation $y = kx$ neatly describes such relationships, where "$k$" represents the constant rate at which quantities change in relation to each other. This equation is vital for translating real-world scenarios into mathematical terms, simplifying problem-solving processes.
Let’s take a look at some real-world examples.
In this scenario, we observe the growth of a plant and how it correlates with the amount of water it receives each week.
Constant of Proportionality ($k$): After dividing the growth by the water for each entry, we find that $k = 3$ cm per litre.
Writing the Equation:
- The general formula for a proportional relationship is $y = kx$.
- Substituting our $k$ value, the equation becomes $y = 3x$.
- This equation represents the relationship: "For every litre of water, the plant grows 3 centimetres."
Let’s observe the relationship between data usage and the number of hours spent online.
Constant of Proportionality (k): Here, $k$ consistently works out to 1.5 GB per hour.
Writing the Equation:
- The proportional relationship is given by $y = kx$.
- Inserting our $k$ value, we get $y = 1.5x$.
- This equation tells us that for each hour spent online, 1.5 GB of data is used.
Try some on your own!
Applying Proportional Relationship Equations
Once you have the equation for a proportional relationship, you can easily find one quantity if you know the other. This is very handy for solving real-world problems. Let's see how it works with some examples.
We can explore how data usage correlates with time spent online. By using the equation $y = 1.5x$, where $y$ is the data used in GB and $x$ is the number of hours spent online, we can find out the total data usage after a specific period of online activity.
- Given Equation: $y = 1.5x$ (Where $y$ is the data used in GB and $x$ is the number of hours spent online)
- Find: How much data is used after 4 hours online?
- Solution: Substitute $x$ with 4 in the equation: $y = 1.5 \times 4 = 6$. So, after 4 hours online, 6 GB of data is used.
In this situation, we're looking at the distance a car can travel over a period of time. Using the equation $y = 60x$, where $y$ represents the distance in miles and $x$ stands for the time in hours, we can determine how far the car travels in a given amount of time.
- Given Equation: $y = 60x$ (Where $y$ is the distance in miles and $x$ is the time in hours)
- Find: How far does a car travel in 3 hours?
- Solution: Substitute $x$ with 3 in the equation: $y = 60 \times 3 = 180$. The car travels 180 miles in 3 hours.
Now, try solving these problems on your own!
Proportional Relationships and Measuring Rates – Summary
Key Learnings from this Text:
- Proportional relationships describe how two quantities change consistently in relation to each other.
- The constant of proportionality ($k$) is a key concept, allowing for the creation of simple equations like $y = kx$ to model these relationships.
- Understanding and applying proportional relationships is crucial for solving real-world problems involving rates, ratios, and direct relationships.
 Do you want to learn faster and more easily?
Do you want to learn faster and more easily?