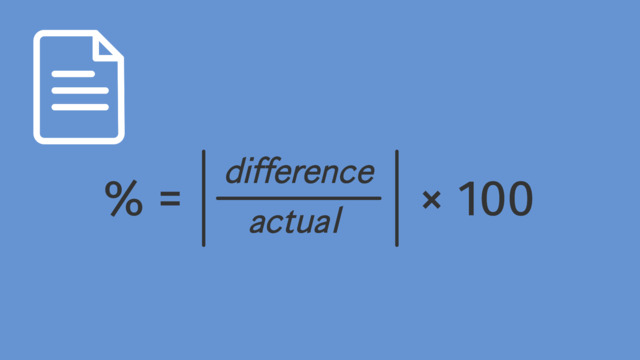Percent Error
Learning text on the topic Percent Error
Percent Error
Percent error is a mathematical tool used to measure the accuracy of a value compared to its true or exact value. It's particularly useful in scientific experiments and everyday calculations where precision is important.
Understanding Percent Error – Explanation
To find the percent error, you need to understand three key terms: the actual value, estimated value, and percent error itself. The actual value is the exact number you're comparing to, while the estimated value is the prediction or measurement you've made.
The formula to calculate percent error is:
Percent Error $=|\dfrac{Actual-Estimated}{Actual}|\times 100$
This formula helps determine how far off an estimate is from the actual value in percentage terms.
| Part of Formula | Description |
|---|---|
| Actual | The true, exact, or correct value that serves as a reference to compare against. |
| Estimated | The measured or predicted value that is being compared to the actual value. |
| Actual - Estimated | The difference between the actual and estimated values, indicating the error in measurement. |
| I Actual - Estimated / Actual I | The absolute value of the difference divided by the actual value, representing the error relative to the actual value. These two vertical lines around the calculation are called the modulus and tell us to take the absolute value. |
| x 100 | Converts the relative error into a percentage, making it easier to interpret the magnitude of the error. |
Just like any formula, once the values are known they can be substituted for the corresponding variables to find the solution, in this case, the percent error.
Converting Decimals to Percents
To find the percent error you will need to remember how to convert a decimal to a percentage. The decimal can be multiplied by $100$ to find the percent. For example, to convert 0.65 to a percent, you would calculate $0.65 \times 100 = 65\%$. This method applies to any decimal and quickly transforms it into an easily understandable percentage. Additionally, you can explore more about these conversions in the section convert between percent, fractions and decimals.
Percent Error – Step-by-Step Process
Steps to Find the Percent Error:
- Identify the actual value.
- Identify the estimated value.
- Substitute these values into the percent error formula.
- Multiply the result by 100 to convert it into a percentage.
Example 1: Suppose a teacher estimates that their classroom is 15 metres long, but the actual length, as measured by a maintenance worker, is 14.8 metres.
- Identify the actual value: The actual length of the classroom is $14.8$ metres.
- Identify the estimated value: The estimated length by the teacher is $15$ metres.
- Substitute these values into the percent error formula: $\text{Percent Error} = \left| \frac{15 - 14.8}{14.8} \right|$
- Multiply the result by 100 to convert it into a percentage: $\left| \frac{15 - 14.8}{14.8} \right| \times 100 \approx 1.35\%$
The percent error in the teacher's estimate is approximately $1.35\%$ to 2.d.p.
Example 2: Sarah estimates that her grocery bill will be $\$$40 dollars, but the actual total comes to $\$38.
- Identify the actual value: The actual cost of the groceries is $38$.
- Identify the estimated value: Sarah's estimated cost is $40$.
- Substitute these values into the percent error formula: $\text{Percent Error} = \left| \frac{40 - 38}{38} \right|$
- Multiply the result by 100 to convert it into a percentage: $\left| \frac{40 - 38}{38} \right| \times 100 \approx 5.26\%$
Sarah's estimation had a percent error of approximately $5.26\%$ to 2.d.p.
Use the percent error formula and try some on your own!
Percent Error – What Does This Number Mean?
Percent error isn't just about finding mistakes; it's a way to understand how precise or accurate your measurements are. This number tells you how much your estimate or measurement has deviated from the actual value in terms of percentage. A higher percent error means a less accurate measurement, while a lower percent error means your measurement is quite close to the true value. Let’s look at what these numbers really mean.
| Percent Error | Description |
|---|---|
| 0% | Perfect! Your measurement or estimate is exactly the same as the actual value. |
| Less than 5% | Excellent accuracy. This is often good enough for most applications, including science class. |
| 5% to 10% | Reasonable accuracy. There's some room for improvement, but it's acceptable for many situations. |
| Greater than 10% | Consider checking how you're measuring. This might be too inaccurate for reliable results, depending on what you're doing. |
Understanding this can help you judge the reliability of your results and see if you might need to change your method or tools.
Example 1: Measuring the height of a plant.
- Person A's estimate: 22 cm
- Person B's estimate: 24 cm
- Actual value: 20 cm
Example 2: Predicting the score of a game.
- Person A's estimate: 50 points
- Person B's estimate: 55 points
- Actual score: 48 points
Example 3: Estimating the number of pages in a book.
- Person A's estimate: 300 pages
- Person B's estimate: 285 pages
- Actual number of pages: 290 pages
Percent Error – Real World Application
Understanding percent error is crucial because it shows us how accurate our measurements or guesses are compared to the real values. Here’s why that’s important:
- Checking Accuracy: It helps you see how close your science experiment measurements are to what they should be. This is like checking if you are hitting the target in archery.
- Improving Techniques: If you know your error is big, you can try different ways to measure more accurately next time. It’s like practising a musical instrument to get better notes.
- Making Better Products: In making things like toys or gadgets, knowing the error helps make sure everything works properly and fits right.
- Better Decisions: In businesses, understanding errors in money estimates can help decide how much to spend or save.
- Enhancing Gaming: Consider playing a virtual reality (VR) game where you need to interact with objects in a virtual environment. If your VR headset doesn't track your movements accurately, it could ruin your experience. Calculating percent error helps improve these technologies, ensuring your actions in the virtual world feel real and responsive.
Percent Error – Summary
Key Learnings from this Text:
- The percent error formula is a valuable tool for measuring the accuracy of measurements against actual values.
- It involves three steps: finding the actual and estimated values, substituting them into the formula, and converting the result into a percentage.
- Once you've calculated the percentage error, compare the actual and estimated values to determine whether your estimate was too high (overestimate) or too low (underestimate), and by how much.
- This concept is useful in both academic settings and everyday life to evaluate and improve measurement techniques.
 Do you want to learn faster and more easily?
Do you want to learn faster and more easily?