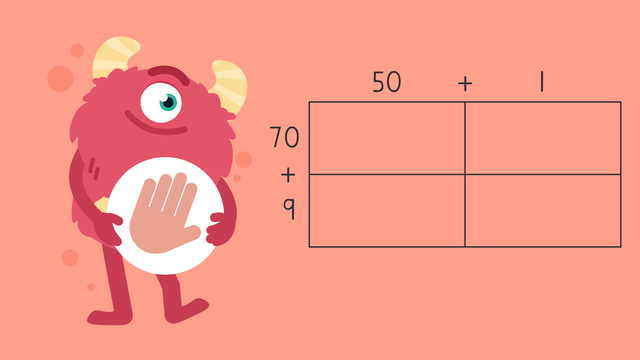
Multiplying 2-Digit Numbers by 2-Digit Numbers Using an Area

Multiplying 2-Digit Numbers by 2-Digit Numbers Using an Area exercise

• The grid method is used as a strategy to solve what kind of equations?

  Hints

  Think about finding the area of a rectangle. What operation would you use?

  The grid method is a strategy used when you are looking to get a larger number.

  Solution

  We use the grid method to solve a multiplication equation. The grid method helps us break down two digit numbers by place value to help us find the product. We can use the grid method as a strategy for finding the product of larger numbers.

• In the equation 45 x 72, what is the expanded form of 72?

  Hints

  Remember, we look at a number from left to right. For example, with the number 67, the 6 is the first digit and it is in the tens place. The 7 is the last digit, and it is in the ones place.

  Draw a grid of you own. What do you notice?

  How would you create the number 72?

  Think about the number 62. The 6 is in the tens place which means the value of the 6 is 60, because it is 6 groups of ten.

  Solution

  The correct answer is 70 + 2. Expanded form means you are writing each factor based on place value. The 7 is in the tens place which means its value is 70, because there are seven groups of ten. The 2 is in the ones place which means its value is 2.

• What are the steps to creating a grid that help us solve 2 digit by 2 digit multiplication?

  Hints

  A grid for multiplying is a rectangle with the expanded form of a number on the top and side.

  Expanded form is when you expand the factors based on the value of the tens and ones place for each number.

  How many place values are in each number?

  Look at the grid. How is it set up?

  Solution

  The steps for solving a multiplication equation using an area model are as follows:

  • First, set up a grid by drawing a rectangle and separating it into parts based on how many place values are in each number. Next, label each side with each factor in expanded form.

  • The second step is to multiply each corresponding pair to find the partial products.

  • Finally, find the sum of all the partial products.

• Solve the equation 34 x 52.

  Hints

  Draw a grid.

  Find partial products and then add them together.

  Solution

  The correct answer is 1,768. Set up your grid by expanding 34 across the top of your box into 30 + 4, and expand 52 into 50 + 2. The next step is to multiply the corresponding boxes to find the partial products: 30 x 50= 1,500 30 x 2= 60 4 x 50 = 200 4 x 2= 8 The last step is to add the partial products together to get your final product: 1,500 + 60 + 200 + 8= 1,768

• Create a grid using the digits that have been provided.

  Hints

  Remember, place means where the digit is located within a number and value means how much the digit is worth.

  Use place value to expand your numbers.

  Here is an example of using the grid method for 58 x 22.

  Solution

  The solution is to expand your factors based on the value. In the factor, 94, the value of the 9 in the tens place is 90. The value of the 4 in the ones place is 4. So you label horizontally across the top, 90 + 4. In the factor, 63, the value of the 6 in the tens place is 60. The value of the 3 in the ones place is 3. So you label vertically down the side, 60 + 3.

  You can also expand 63 across the top as 60 + 3, and expand 94 along the side as 90 + 4. It does not matter which number you expand across the top versus along the side, as long as you expand them correctly.

• Complete the equations.

  Hints

  Remember, once you have expanded the number, you multiply the corresponding pairs to find the partial products.

  Multiply each corresponding box one at a time to avoid making a mistake.

  To find the final product, what operation do you use?

  Solution

  Since you were already given the expanded form, you skip that step and go right to the next step which is to multiply each corresponding pair to find a partial product.

  For the grid on the left, we find the following partial products:

  • 80 x 40 = 3,200

  • 2 x 40 = 80

  • 80 x 6 = 540

  • 2 x 6 = 12

  For the grid on the right, we find the following partial products:

  • 20 x 10 = 200

  • 9 x10 = 90

  • 20 x 6 = 120

  • 9 x 6 = 54

  After finding the partial products, you add them together to find the final product.

  So 82 x 46 would be: 3,200 + 80 + 80 x 6 + 12 = 3,932

  29 x 16 would be: 200 + 90 + 120 + 54 = 464