Fractions with the Same Denominator

Basics on the topic Fractions with the Same Denominator
Learn all about comparing fractions with the same denominator in this video.
Transcript Fractions with the Same Denominator
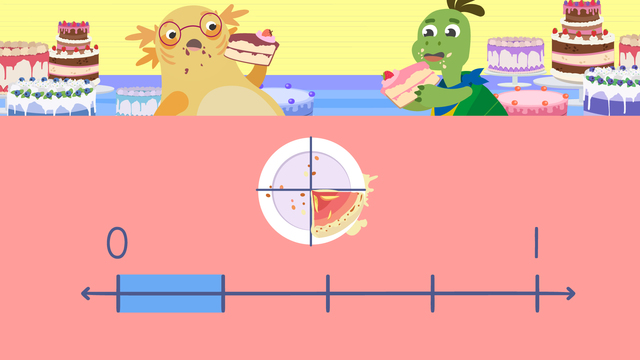
Axel and Tank are working on puzzles of identical size. Axel has ten of the twelve pieces in place. Tank has nine of the twelve pieces in place. They want to compare who's finished more, so we'll need to teach them about "Comparing Fractions with the Same Denominator". Denominators tell us how many equal parts a whole is divided into. Here is an example of fractions with the SAME denominators. The fraction with the greatest numerator will always be larger when comparing fractions with the same denominator. This is because each part is the same size, and the greater numerator is telling us we have MORE of the equal parts.
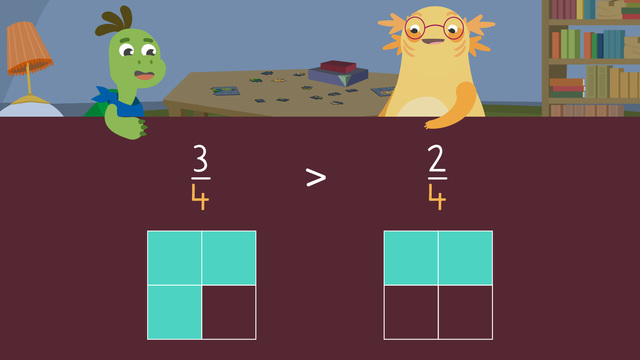
Fraction models can help us see if fractions with the same denominator are greater than, less than, or equal to one another. Let's compare these fractions with the same denominator. Three quarters and two quarters. They both have the same denominator and come from the same whole. First, draw and shade a fraction model to represent three quarters. Then, draw and shade another identical fraction model to represent two quarters. Finally, compare the shaded values of both models. Three quarters has MORE parts shaded than two quarters. So three quarters is GREATER THAN two quarters. Remember, when looking at fractions with the same denominator, the GREATER numerator is larger. Now let's take a look at Axel and Tank's puzzle progress. We have eight twelfths and ten twelfths. First, draw and shade a fraction model to represent eight twelfths. Then, draw and shade another identical fraction model to represent ten twelfths. Finally, compare the shaded values of both models. Eight twelfths has FEWER parts shaded than ten twelfths. So, eight twelfths is LESS THAN ten twelfths. The fraction with the smallest NUMERATOR is smaller. Let's try this again using the progress from Axel and Tank's LAST puzzles. Tank has eleven fifteenths finished and Axel has nine fifteenths finished. Who has more of their puzzle done?
Tank has more of his puzzle done because the numerator is greater than Tank's. How can we check our answer? We can use fraction models! First, draw and shade a fraction model to represent eleven fifteenths. Then, draw and shade another identical fraction model to represent nine fifteenths. Finally, compare the shaded values of both models. Eleven fifteenths has more parts shaded than nine fifteenths, so eleven fifteenths is greater than nine fifteenths. Tank HAS done more of his puzzle than Axel! While Axel and Tank finish their puzzles, let's review!
When working with fractions with the same denominator, the fraction with the LARGEREST numerator will always be larger. We can check our work by setting up identical fraction models. First, draw and shade a fraction model to represent the first fraction. Then, draw and shade another identical fraction model to represent the second fraction. Finally, compare the shaded values of both models. The fraction with more shaded parts is greater! Axel and Tank have both finished their last puzzle now! But why do THEY look puzzled? "Tank, do you think some of our pieces got shuffled?"
Fractions with the Same Denominator exercise
-
When comparing fractions with identical wholes, the fraction with the greater numerator will always be _______.
HintsWhich fraction has more equal parts shaded in here?
Remember, each part is the same size and the greater numerator is telling us we have more of the equal parts.
SolutionWhen comparing fractions with identical wholes, the fraction with the greater numerator will always be larger.
Fractions with identical wholes have the same denominator. You can see this in the image above. Each part is the same size and the greater numerator is telling us we have more of the equal parts (more parts are shaded in).
-
Which expressions are true?
HintsRemember, when comparing fractions with the same denominator, the larger numerator will always be the larger fraction.
< means less than, and > means greater than.
When looking at the fraction models, which fraction has more equal parts shaded in? That will be the larger fraction.
For example, $\frac{3}{4}$ is greater than $\frac{2}{4}$.
SolutionShown are the correct expressions. Remember, when comparing like fractions with the same whole, the larger numerator will also be the larger fraction.
The first expression is incorrect, because $\frac{1}{3}$ is < $\frac{2}{3}$
The second expression is correct, because $\frac{3}{6}$ is < $\frac{4}{6}$
The third expression is incorrect, because $\frac{7}{8}$ is > $\frac{6}{8}$
The fourth expression is correct, because $\frac{5}{6}$ is > $\frac{4}{6}$
-
Comparing fractions.
HintsWhen looking at the fraction models, which fraction has more equal parts shaded in? That will be the larger fraction.
e.g. $\frac{3}{4}$ > $\frac{2}{4}$
Remember, when comparing fractions with the same denominator, the larger numerator will always be the larger fraction.
< means less than, and > means greater than.
SolutionRemember, when comparing fractions with the same denominator, the larger numerator will also be the larger fraction.
$\frac{3}{3}$ > $\frac{2}{3}$
$\frac{1}{6}$ < $\frac{2}{6}$
$\frac{2}{8}$ < $\frac{3}{8}$
$\frac{6}{8}$ > $\frac{5}{8}$
-
Who ate more pizza?
Hints< means less than, and > means greater than.
Make sure you're looking at how many pieces are shaded in.
SolutionFor the first set: $\frac{2}{5}$ < $\frac{3}{5}$
For the second set: $\frac{5}{7}$ < $\frac{6}{7}$
For the third set: $\frac{4}{8}$ = $\frac{4}{8}$
-
Which option shows fractions with the same denominator?
HintsRemember, the bottom number is the denominator.
Here is an example of fractions with the same denominator.
Solution$\frac{1}{3}$ and $\frac{2}{3}$ are fractions with the same denominator.
The denominator is the bottom number in a fraction.
-
Greater than or less than?
HintsRemember, when comparing fractions with the same denominator, the larger numerator will always be the larger fraction.
< means less than, and > means greater than.
Solution$\frac{5}{6}$ < $\frac{6}{6}$
$\frac{4}{6}$ < $\frac{5}{6}$
$\frac{2}{8}$ > $\frac{1}{8}$
$\frac{4}{8}$ > $\frac{3}{8}$


 Do you want to learn faster and more easily?
Do you want to learn faster and more easily?