Tenths and Hundredths
Basics on the topic Tenths and Hundredths
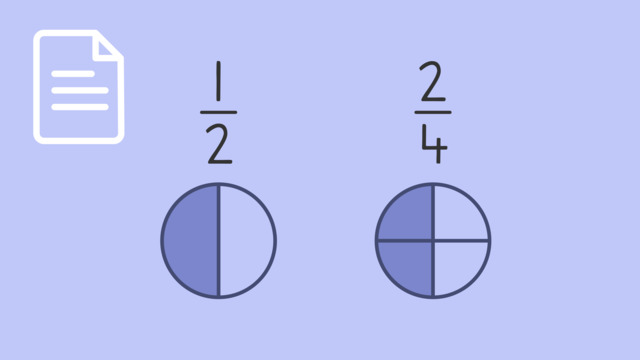
Equivalent Decimal Fractions
A fraction is a portion or part of any quantity out of a whole. There are different types of fractions including: improper fractions, mixed fractions, proper fractions and decimal fractions.
In this video we will learn about decimal fractions and how to identify equivalent decimal fractions as well as how to write decimal fractions. We will show a couple of examples after which you can practise a set of decimal fractions problems with ease.
Revision – Decimal Fractions
Let’s recap what decimal fractions are first:
Decimal fractions are fractions where the denominator is a power of ten. A power of ten means multiplying ten by itself a certain number of times. For example, 10 x 10 = 100, and 10 x 10 x 10 = 1,000.
Equivalent Decimal Fractions – Definition
Equivalent decimal fractions are fractions that are equal in value and the denominator is a power of ten. For example, fractions with denominators of 10, 100, 1,000 and so on.
Comparing Decimal Fractions – Examples
A great visual method to compare decimal fractions is to use base 10 blocks. Below are some examples.
Comparing Decimal Fractions – Example 1
In this first base 10 block the whole is divided into ten equal parts, so the denominator is ten. Four out of ten parts are shaded in blue; so we label the shaded parts in the numerator as four, making the decimal fraction $\frac{4}{10}$.
On the other base 10 block, the whole is divided into one hundred equal parts, so the denominator is one hundred. Forty sections out of one hundred parts are shaded in red which we can represent as the decimal fraction $\frac{40}{100}$. The base 10 blocks below help us when comparing fractions with denominators of 10 and 100.
We can convert fractions with denominators of 10 and 100 to decimals. Our $\frac{4}{10}$ and $\frac{40}{100}$ can be written as 0.4 = 0.40.
| Denominator 10 | Denominator 100 | |
|---|---|---|
| fraction | $\frac{4}{10}$ | $\frac{40}{100}$ |
| decimal | 0.4 | 0.40 |
Comparing Decimal Fractions – Example 2
Let’s look at different examples to clarify our understanding of equivalent fractions with denominators of 10 and 100. Equivalent fractions and decimals with denominators of 10 and 100 are more comprehensible if we visualize them.
In this base 10 block the whole is divided into one hundred equal parts, and ninety out of one hundred parts are shaded in red which we can write as a decimal fraction $\frac{90}{100}$.
In the second base 10 block the whole is divided into ten equal parts, and nine out of ten parts are shaded in blue, so we can represent the shaded parts as a decimal fraction $\frac{9}{10}$.
The base 10 blocks represent two equivalent fractions with denominators of 10 and 100.
| Denominator 10 | Denominator 100 | |
|---|---|---|
| fraction | $\frac{9}{10}$ | $\frac{90}{100}$ |
| decimal | 0.9 | 0.90 |
Equivalent Decimal Fractions – Summary
How do we compare decimal fractions? Look at the summary below:
- Look at each of the base 10 blocks
- Set up each fraction and label the denominators based on how many parts each base 10 block is broken into
- Look at the shaded parts of each base 10 block
- Label the numerator with the number of shaded parts in each base 10 block
- Use the less than, greater than, or equal to symbol to record your answer
You can also look at our worksheets and videos on equivalent decimal fractions with denominators of 10 and 100 for more practice. We also provide worksheets on adding fractions with denominators of 10 and 100 as well as place value and decimal fractions worksheets. Soon you’ll be able to answer questions like “what is a fraction with a denominator of 10?” and “what is a fraction that has a denominator of 100?” easily!
##Frequently Asked Questions on Equivalent Decimal Fractions
Transcript Tenths and Hundredths
"Doo dee do do doo, oh, what does this button do Axel?!" "Tank, don't push that!" Axel and Tank need to get back home. However, they need to crack the codes to unlock the doors. Let's help them by identifying, Equivalent Fractions: tenths and hundredths. Tenths and hundredths can be compared by multiplying or dividing by ten as ten times ten is one hundred and one hundred divided by ten is ten. Equivalent fractions are fractions that are equal in value. We can compare these fractions using base ten blocks. For example, near the first door we see four tenths. This base ten block represents tenths, because the whole is broken up into ten equal parts and since four out of ten parts are shaded, the numerator is four. To unlock the door, we need to identify a fraction out of one hundred that is equivalent to four tenths. The denominator of the equivalent fraction is one hundred, because we see here the whole is broken up into one hundred equal parts. That means this base ten block represents hundredths. In order to identify the numerator, we shade the same value, or amount, as four tenths on the base ten block. How many hundredths are shaded in? Forty, because there are four columns with ten in each shaded. Four tenths is equal to forty hundredths because the same value is shaded in. We can also see that we have multiplied both the numerator and the denominator by ten . So Axel and Tank go to the next door. Here, we need to identify a fraction in tenths that is equivalent to ninety hundredths. What is the denominator? This whole is divided into tenths, so the denominator is ten. How many tenths do we shade in to make an equivalent fraction? In order to be equivalent, the same value must be shaded in, so we shade in nine. As we have divided our denominator by ten, we also divide the numerator by ten. Ninety divided by ten equals nine, and write it here. Ninety hundredths is equal to nine tenths because the same value is shaded in. Axel and Tank head to the last door. This time, we need to write the fraction represented as tenths and then find the equivalent fraction out of one hundred. Try solving on your own. Pause the video so you have time to work and press play when you're ready to see the steps for finding the answer! First, write seven tenths here because there are seven tenths shaded on the base ten block. Since there are one hundred parts in our whole, write the denominator one hundred here. We can also see that we have multiplied the denominator by ten to get one hundred. Next shade in seventy hundredths because both blocks need to have the same value in order to be equivalent. If we also multiply our numerator by ten, we get seventy. So seven tenths is equal to seventy hundredths. Before we see if Axel and Tank have made it back home, let's summarise. Remember, we can compare fractions written as tenths and hundredths by using base ten blocks. In order to identify equivalent fractions, first write the denominator. Secondly, shade in the same value on the other base ten block. Finally, count how much you shaded in, and write the result as the numerator. "Wait this isn't our home, but it looks a lot like it!" "Yeah, really nice choice on the decor Mrs. Loch Ness Monster. Oh what does this button do?!?" "Tank, please, not again!"
Tenths and Hundredths exercise
-
What does equivalent mean when we are talking about fractions?
HintsRemember to look at the shading in the picture. Are they the same? Does one have more than the other?
The fractions we see in the previous hint are equivalent to each other: $\dfrac{4}{10}$ is equivalent to $\dfrac{40}{100}$.
SolutionEquivalent means equal to or the same as. When two fractions are different but have the same value, they are equivalent.
-
Can you identify the correct base ten blocks?
HintsRemember, you are finding the fraction represented in tens or hundreds blocks. Look at the denominator to see whether you are matching to tens or hundreds.
The numerator is represented by the amount of blocks shaded in.
Solution- There are 2 out of 10 bars filled in, which represents the fraction $\dfrac{2}{10}$.
- There are 70 out of 100 boxes filled in, which represents the fraction $\dfrac{70}{100}$.
- There are 5 out of 10 bars filled in, which represents the fraction $\dfrac{5}{10}$.
- There are 10 out of 100 boxes filled in, which represents the fraction $\dfrac{10}{100}$.
-
What is the fraction represented on the base ten block?
HintsRemember that the numerator represents the number of boxes shaded.
As an example, these base ten blocks illustrate $\frac{4}{10}$.
Solution1.The first image represents $\frac{8}{10}$. 8 of the 10 boxes are shaded in.
2.The second image represents $\frac{50}{100}$. 50 of the 100 boxes are shaded in.
3.The third image represents $\frac{80}{100}$. 80 of the 100 boxes are shaded in.
4.The fourth image represents $\frac{5}{10}$. 5 of the 10 boxes are shaded in.
-
Can you find the equivalent fractions?
HintsThese images will help you to find one of the pairs above. They are equivalent fractions.
Remember:
- The shaded part represents the numerator.
- The total number of boxes represents the denominator.
Remember that we can also think of these numbers as being multiplied by 10.
For example, $\frac{4}{10}$ = $\frac{40}{100}$ When we multiply 4 by 10 we get 40, and when we multiply 10 by 10 we get 100. These are equivalent fractions.
Solution$\frac{9}{10}$ = $\frac{90}{100}$
We can see on the shaded blocks that 9 of the 10 blocks are shaded, which looks the same as 90 of the 100 blocks that are also shaded. If we were to lay one on top of the other the same amount would be shaded in, making them equivalent.
_____________________________________________________
$\frac{6}{10}$ = $\frac{60}{100}$
$\frac{2}{10}$ = $\frac{20}{100}$
$\frac{1}{10}$ = $\frac{10}{100}$
-
What is the missing fraction?
HintsWe can tell from looking at the base ten block images if this is an equivalent fraction or not.
The numerator is represented by the number of blocks shaded in.
Remember, the total number of boxes the square is divided into represents the denominator, or the number that goes in the bottom half of the fraction.
SolutionThe second fraction represents our original fraction changed into a hundredth denominator. 30 out of 100 blocks are filled in, so $\frac{3}{10}$ becomes $\frac{30}{100}$. The two fractions are equivalent.
-
How much pizza have Axel and Tank eaten after their adventure?
HintsRemember that the pizza is similar to the base ten block. Look at the pizza represented in a base ten block.
Remember, the numerator is the number of pieces eaten and the denominator is the total number of pieces of pizza.
If we multiply 4 x 10 we get 40.
If we multiply 10 x 10 we get 100.
What do you get if you multiply:
- 40 x 10?
- 100 x 10?
SolutionCount all of the pieces of the pizza. There are 10 in total. Of those 10, how many are missing? There are 4 pieces of pizza missing. That means that Axel and Tank ate 4 pieces out of 10, or they ate $\frac{4}{10}$ of the pizza.
$\dfrac{4}{10}$ = $\dfrac{40}{100}$ = $\dfrac{400}{1000}$
- 4 x 10 = 40
- 10 x 10 = 100
- Therefore: $\frac{4}{10}$ = $\frac{40}{100}$
- 40 x 10 = 400
- 100 x 10 = 1000
- Therefore: $\frac{40}{100}$ = $\frac{400}{1000}$

 Do you want to learn faster and more easily?
Do you want to learn faster and more easily?