Simplifying Fractions — Let's Practise!

Basics on the topic Simplifying Fractions — Let's Practise!
Today we are practising simplifying fractions with Razzi! This video contains examples to help you further practise and grow confident in this area.
Transcript Simplifying Fractions — Let's Practise!
Razzi says get these items ready because today we're going to practise simplifying fractions.It's time to begin! Which fraction can four-twentieths be simplified to? Two-fifths, one-fifth, one-quarter. Pause the video to work on the problem and press play when you are ready to see the solution! The common factor of four and twenty is four. Four divided by four is one and twenty divided by four is five. Did you also get one-fifth? Let's tackle the next problem! Which fraction can eighteen-twenty-sevenths be simplified to? Two-thirds four-fifths nine-twelfths. Pause the video to work on the problem and press play when you are ready to see the solution! The common factor of eighteen and twenty-seven is nine. Eighteen divided by nine is two and twenty-seven divided by nine is three. Did you also get two-thirds? Let's try one more! What is the simplified fraction of thirty-five over forty-two. Four-fifths, seven-eighths, five- sixths. Pause the video to work on the problem and press play when you are ready to see the solution! The common factor of thirty-five and forty-two is seven. Thirty-five divided by seven is five and forty-two divided by seven is six. Did you also get five-sixths? Razzi had so much fun practising with you today! See you next time!
Simplifying Fractions — Let's Practise! exercise
-
True or False?
HintsTo check if the fractions are correct, count the number of highlighted (dark green) blocks and the total number of blocks.
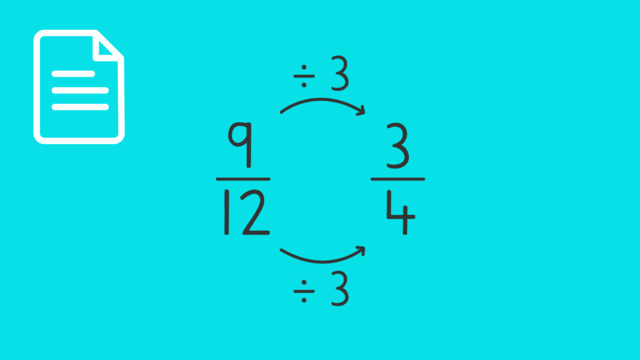
On the left, there are 4 highlighted blocks and 12 blocks altogether, representing the fraction $\frac{4}{12}$.
Equivalent means equal.
Do both fractions represent the same amount?
The greatest common factor is the largest number that both 4 and 12 are divisible by.
Solution- True. Left fraction: $\frac{4}{12}$, right fraction: $\frac{1}{3}$
- True. The two fractions are equivalent.
- False. The greatest common factor of 4 and 12 is not 2.
- To find the greatest common factor, list the numbers that both 4 and 12 are divisible by. They are: 1, 2 and 4. Therefore, the greatest common factor is 4.
-
Simplify the fraction.
HintsList all common factors that the numerator and denominator share. Which is greatest?
Divide the numerator and denominator by the greatest common factor to get the simplified fraction.
SolutionThe greatest common factor is 5.
In the simplified fraction, the numerator is 1 and the denominator is 4.
The simplified fraction is $\mathbf{\frac{1}{4}}$.
-
Can you find the greatest common factor?
HintsList all common factors that the numerator and denominator share.
Choose the largest factor from the list to find the greatest common factor.
The factors of 28 and 35 are:
28: 1, 2, 4, 7, 14, 28
35: 1, 5, 7, 35
What is the largest factor they both share?
Solution1) $\frac{12}{16}$: The greatest common factor is 4.
2) $\frac{15}{18}$: The greatest common factor is 3.
3) $\frac{28}{35}$: The greatest common factor is 7.
4) $\frac{24}{39}$: The greatest common factor is 3.
-
Can you simplify these fractions?
HintsDivide the numerator and denominator by the greatest common factor.
List all factors for 35 and 56:
35: 1, 5, 7, 35
56: 1, 2, 4, 7, 8, 14, 28, 56
Divide both numbers by the greatest factor they both share to simplify the fraction.
Solution$\frac{27}{36}$: The greatest common factor is 9. The simplified fraction is 3 over 4 or $\frac{3}{4}$.
$\frac{20}{28}$: The greatest common factor is 4. The simplified fraction is 5 over 7 or $\frac{5}{7}$.
$\frac{35}{56}$: The greatest common factor is 7. The simplified fraction is 5 over 8 or $\frac{5}{8}$.
-
Simplify the fraction.
HintsTo find the unsimplified fraction shown by the blocks:
- Count the number of highlighted blocks. Write this number on the top of the fraction.
- Count the total number of highlighted and non-highlighted blocks. Write this number on the bottom.
There are 4 shaded blocks and 6 blocks altogether, what is the fraction represented?
To find the greatest common factor, list all of the factors of 4 and 6.
Which numbers can both the numerator (4) and denominator (6) be divided by?
Divide 4 and 6 by their greatest common factor to find the simplified fraction.
Solution- The unsimplified fraction is $\frac{4}{6}$.
- The greatest common factor is 2.
- The numerator of the simplified fraction is 2.
- the denominator of the simplified fraction is 3.
- The simplified fraction is $\frac{2}{3}$.
-
Solve the word problem.
HintsThis is a daisy.
Start by writing out the unsimplified fraction.
The number of daisies is the numerator.
The total number of all flowers is the denominator.
Next, simplify the fraction.
Divide both the numerator and denominator by the greatest common factor.
SolutionThe fraction of daisies in the total bouquet is 3 over 8 or $\frac{3}{8}$.
The unsimplified fraction is $\frac{12}{32}$. Divide each number by 4 (the greatest common factor of 12 and 32) to get the simplified fraction, $\frac{3}{8}$.


 Do you want to learn faster and more easily?
Do you want to learn faster and more easily?