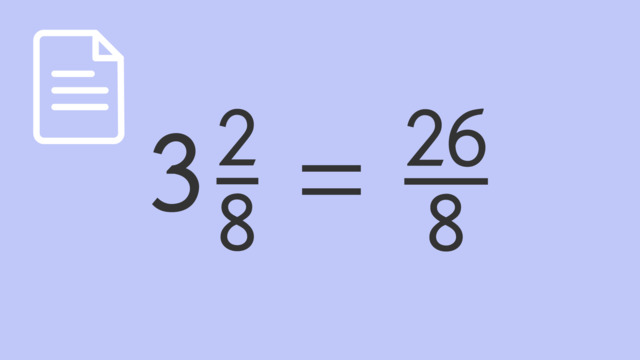Interpreting Fractions as Division
Do you want to learn faster and more easily?
Basics on the topic Interpreting Fractions as Division
Learn how to rewrite fractions as a division sentence and find fractions of amounts by using division!
Transcript Interpreting Fractions as Division
Sometimes when we share things, we have less to distribute than the number we are sharing between. And that might seem tricky to solve, but it doesn't have to be! Interpreting fractions as division. You may remember that fractions consist of two parts; the numerator and the denominator. The denominator, ‘B’, tells us how many equal parts the whole is divided into, and the numerator, ‘A’, tells us how many parts of the whole we have. Let's explore how we can rewrite a fraction as a division sentence. Imagine that you have a whole pizza, and you want to share it equally among four people. That means you need to divide the whole pizza into four equal parts. When we write this as a division sentence, it is one divided by four. This would mean that each person gets an equal part of the pizza, which can be rewritten in fraction form as one over four. This is how we can interpret a division as a fraction, and also a fraction as a division sentence! Let's take a look at another example. This time, we have three rolls, and we are sharing them between five people. Let's use fraction bars to help us make sense of this one. As you may already notice, each person this time would get three-fifths of a roll. Let's make sure this division works by using fraction bars. If we divide each roll into fifths, we can see that if we distribute each part equally between the five friends, we end up with three parts per person, or three fifths. Now it's your turn! If you have two chocolate bars, and you share them among three people, what fraction of chocolate does each person get? Pause the video to solve, and press play when you are ready to see the solution. Since we are dividing two by three, each person gets two thirds of a chocolate bar. Here is one more problem. This time, we have the fraction four eighths. What is the division sentence that matches this fraction? Pause the video to solve, and press play when you are ready to see the solution. Four eighths tells us that we have four whole things to share between eight, so it is four divided by eight. To summarise, the fraction ‘A’ over ‘B’ can be rewritten as ‘A’ divided by ‘B’, and ‘A’ divided by ‘B’ can be rewritten as a fraction ‘A’ over ‘B’. Fractions represent dividing a whole into equal parts. So now, whenever you see a fraction, think of it as a division problem, and you can make sense of fractions!
Interpreting Fractions as Division exercise
-
What are the fraction parts?
HintsThe top of the fraction is called the numerator and is how many parts of the whole we have. For example, if we had one slice of this pizza we would put $1$ on the top of the fraction.
The bottom of the fraction is called the denominator.
Solution- $a$ is the numerator and is how many parts of the whole we have
- $b$ is the denominator and is how many equal parts the whole is divided into
-
Convert division to a fraction.
Hints- The top (numerator) of the fraction is how many parts we have.
- The bottom (denominator) of the fraction is how many equal parts the whole is divided into.
The numerator $a$, is the number of slices we have and the denominator $b$ is the number of equal slices the pizza is cut into. For example, one slice of this pizza is $1\div5 = \frac{1}{5}$.
Solution$1\div10 = \frac{1}{10}$
One slice of pizza out of a total of $10$ equal slices.
-
Using division to represent a fraction of chocolate.
HintsEach chocolate bar should be split into $4$, as there are $4$ people to share the chocolate.
Use bars to split it.
When the chocolate is split into $4$, each person gets $1$ out of $4$.
We do this $3$ times as there are $3$ bars of chocolate.
We are sharing $3$ chocolate bars with $4$ people.
$3\div4$
SolutionEach person gets $3\div4 = \frac{3}{4}$ of a bar of chocolate.
-
Using division to represent a fraction of cola.
HintsEach bottle should be shared into $7$.
There are $5$ bottles, each shared into $7$. Each friend would get $\frac{1}{7}$ from each bottle, so we multiply this by $5$ (bottles).
Solution$\frac{5}{7} = 5\div7$
There are $5$ bottles each shared into $7$, that is $5\div7$.
-
Convert the fractions to division.
Hints- The top (numerator) of the fraction is how many parts we have.
- The bottom (denominator) of the fraction is how many equal parts the whole is divided into.
- As a division sentence we would write ${numerator}\div{denominator}$.
$\frac{numerator}{denominator} = {numerator}\div{denominator}$
For example, one slice of this cake could be written as $\frac{1}{8} = 1\div8$.
Solution- $\frac{2}{3} = 2\div3$
- $\frac{1}{2} = 1\div2$
- $\frac{1}{3} = 1\div3$
- $\frac{1}{5} = 1\div5$
- $\frac{3}{5} = 3\div5$
${}$
$\dfrac{numerator}{denominator} = {numerator}\div{denominator}$.
For example, one slice from two is $\dfrac{1}{2} = 1\div2$ as above.
-
Determine the fraction when dividing pizza.
HintsEach pizza should be split into the number of friends. For example, if there were $8$ friends the pizza would be split into $8$.
When the pizza has been split into the number of friends we multiply the fraction by $4$, as we have $4$ pizzas.
For example, $\frac{1}{13}\times4 = \frac{4}{13}$
Solution- $5$ friends $= 4\div5 = \frac{4}{5}$
- $6$ friends $= 4\div6 = \frac{4}{6}$
- $12$ friends $= 4\div12 = \frac{4}{12}$
- $9$ friends $= 4\div9 = \frac{4}{9}$
