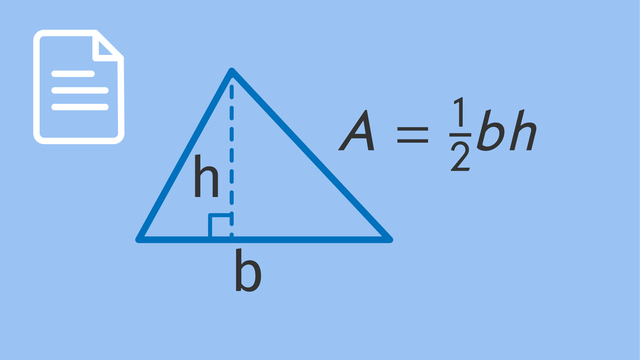Finding the Area of an Acute Triangle
Learning text on the topic Finding the Area of an Acute Triangle
Finding the Area of Acute Triangles
In this text, we're learning how to find the area of acute triangles. These are triangles where all of the angles are smaller than 90 degrees. Knowing how to do this is useful, not just in maths lessons but for real-life stuff too, like planning out a garden or figuring out the shape of a sail.
Plus, there's a cool thing about triangles: whether they are acute, obtuse or right angled triangles, you can use the same simple formula to figure out their area. This makes understanding triangles a bit easier and shows how maths can be pretty handy in the real world.
An acute triangle is defined by having all three interior angles less than 90 degrees.
Classifying triangles by angles is necessary when distinguishing between acute, obtuse and right angled triangles.
Types of Acute Triangles
Acute triangles can be further classified based on their side lengths. This classification helps in understanding the properties and solving problems related to these triangles more effectively. Here is a brief overview:
| Type | Description | Characteristics |
|---|---|---|
| Equilateral Acute Triangle | All three sides are of equal length, and all three angles are equal, measuring 60 degrees each. | - All sides equal - All angles are 60° |
| Isosceles Acute Triangle | Two sides are of equal length, and the angles opposite these sides are also equal. Typically, these triangles have two acute angles and one angle that could be acute or obtuse, but in the context of an acute triangle, all angles are less than 90 degrees. | - Two sides equal - Two angles equal |
| Scalene Triangle | All three sides and all three angles are of different lengths and measures, respectively. | - No sides are equal - No angles are equal |
Area of a Triangle Formula
The area of an acute triangle is found using the formula: $A=\frac{1}{2}bh$, where $b$ is the base's length, and $h$ is the height, measured perpendicularly from the base.
Base and Height of Acute Triangles
In geometry, especially when working with triangles, two key terms we often encounter are the base and the height. Understanding these terms is crucial for solving various problems, including finding the area of triangles.
Base: The base of a triangle is any one of its sides that we use as a reference point for measurement. When calculating the area, you can choose any side as the base, but typically, it's the bottom side when the triangle is drawn on paper.
Height: The height (or altitude) of a triangle is a perpendicular line segment from the base to the opposite vertex. The height measures how tall the triangle is from its base to its highest point.
Finding the Area of an Acute Triangle – Step-by-Step Process
| Step | Description | Example |
|---|---|---|
| 1. Identify the Formula and Base/Height | Start by recognising the formula for the area of a triangle, which is $A = \frac{1}{2}bh$. Then, identify which side of the triangle will serve as the base ($b$) and the perpendicular height ($h$) from that base. | For our example, let's use a triangle with a base ($b$) of 8 cm and a height ($h$) of 5 cm. |
| 2. Substitute the Values into the Formula | Plug the values of the base and height into the formula to prepare for calculation. | Substitute the values into the formula: $A = \frac{1}{2}(8 \text{ cm})(5 \text{ cm})$. |
| 3. Calculate and Add Units for the Final Answer | Perform the multiplication and division as indicated by the formula to find the area. Remember to include the correct units in your final answer, which will be in square units. | Calculate the area: $A = \frac{1}{2}(8 \text{ cm})(5 \text{ cm})$ $A=\frac{1}{2}(40 \text{ cm})$ $A=20 \text{ cm}^2$ The area of the triangle is $20 \text{ cm}^2$. |
Let’s look at another example.
Find the area of the triangle.
Finding the Area of an Acute Triangle – Practice
Use the steps to find the area of more acute triangles on your own!
Acute Triangle Area – Summary
Key Learnings from this Text:
- The formula $A=\frac{1}{2}bh$ is essential for calculating the area of an acute triangle.
- Base is defined as any side of the triangle that is considered the reference or bottom side for the calculation.
- Height is the perpendicular distance from the base to the opposite vertex, crucial for determining the triangle's area accurately.
- Understanding and applying this formula enhances geometric understanding and problem-solving skills.
- Regular practice with triangles of various sizes and configurations builds proficiency and confidence in these calculations.
Learn more with our text on finding the area of right angled triangles.
 Do you want to learn faster and more easily?
Do you want to learn faster and more easily?