Describing Patterns in Scatter Graphs
Basics on the topic Describing Patterns in Scatter Graphs
Find out about different ways you can describe patterns in scatter graphs.
Transcript Describing Patterns in Scatter Graphs
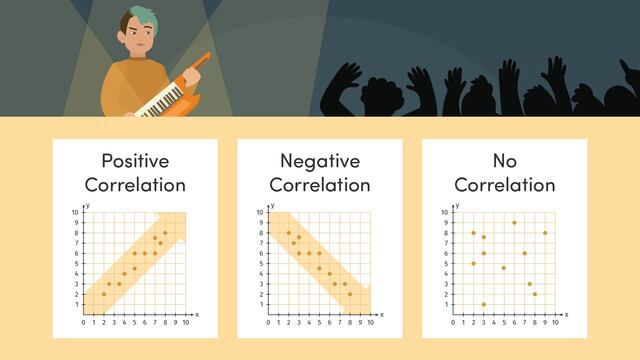
Kai is getting excited, but also nervous about his first keytar performance in front of hundreds of people. Let's rewind time first and learn more about, describing patterns in scatter graphs to discover different relationships in the events leading up to the big day. To review, a scatter graph is a graph that displays the relationship between two sets of data. We can find patterns between the X and Y values that define their relationship and make predictions. The relationship has a positive correlation, when both the X and Y values increase. For example, the more time you spend exercising, the more calories you burn. The relationship has a negative correlation when the X value increases, and the Y value decreases. For example as the temperature outside increases, hot chocolate sales decrease. No correlation means that the X and Y values have no relationship. For example, age has no effect on the number of siblings you have. Some scatter plots have outliers, which is a point that does not fit the pattern. Clusters are data points that form a group. Let's get back to Kai's big keytar performance! Leading up to the big day, Kai practised weekly. Each week, he recorded the hours he practised as the X variable, and compared that to his weekly assessment score Y. This scatter graph shows the relationship between the number of hours Kai practised and the score on his weekly assessment. Let's describe any patterns we see in this scatter graph. This scatter graph has a positive correlation, you can see the points are trending upwards, and as the X value increases, the Y value also increases. There is also one outlier in this graph when Kai practised for five hours, his score was less than twenty-five percent and this one does not fit the pattern. This scatter graph also happens to have a cluster of points. What has Kai learnt from this pattern? The more he practises, the higher his assessment score will be. On the day of the performance, Kai along with the band, will get a bus to the venue. The drive is over twenty miles, and this scatter graph shows the relationship between the miles driven and the amount of petrol left. This scatter graph shows a negative correlation since the points show a downwards pattern. There are no outliers or clusters. The relationship is that as the X value or miles driven increases, the Y value or gallons of petrol in the tank decreases. When the bus ran out of petrol, they stopped at a petrol station. During the stop, the band members took a survey and made a scatter graph showing the relationship between their ages X, and the number of snacks they packed Y. Pause the video here and identify the pattern of ages to snacks. There is no correlation between the ages and snacks. Also, there are no outliers or clusters. This means that how old you are has no effect on how many snacks are packed for a bus ride. To summarise, a scatter graph displays a relationship between two data sets which we can then analyse. The relationships can either be positive, negative or have no correlation. We can also identify outliers and clusters in a scatter graph to help us learn more about the data. Oh! Shhhh, get ready, here comes Kai!
Describing Patterns in Scatter Graphs exercise
-
What is a scatter graph?
HintsA scatter graph displays a relationship between two sets of data.
If you are not sure, count the number of data categories in each graph.
Data plotted into a scatter graph is given a point for two variables.
For example, person A, weight and height, person B weight and height etc.
SolutionAs a scatter graph displays a relationship between two sets of data, this is the only one which does that.
You can see the y-axis is ice cream sales and the x-axis is the temperature that day.
-
Find the correlation.
HintsNegative correlation means that as one value increases, the other value decreases.
An example of this would be, 'as the cakes on the plate decrease, the fuller I would get'.
This is a scatter graph with negative correlation.
The $x$ values increase while the $y$ values decrease.
There are three correct answers here.
SolutionThese are all negatively correlated because as one value increases the other decreases.
- miles travelled in the car and the level of petrol in the tank
- sales of winter coats and the temperature of the day
- number of sweets left in the bag and the number of sweets eaten
-
Find the outlier.
HintsAn outlier is different to the other data points.
On a scatter graph it would not follow the trend of the others and would stand out.
An outlier would look like this on a scatter graph.
SolutionTemperature $26^\circ$C, $50$ ice creams sold
It would not follow the pattern of the others on the scatter graph.
-
No correlation.
HintsWhen a relationship has no correlation it means the two data sets are completely unrelated. They could be easy to spot because they appear a bit silly.
For example, a person's height and the length of time watching TV have no correlation.
The scatter graph looks like this when there is no correlation
We can see there is no pattern to the data.
There are three answers that have no correlation.
SolutionAll these are unrelated to each other and do not have correlation:
- Hair length and number of hours on social media
- Height and amount of pets a person has
- Number of illnesses a person has had and number of shoes a person owns
-
What type of relationship is displayed?
HintsThere are 3 types of correlation.
Decide which is similar to the data displayed above.
- Positive correlation: as the $x$ value increases, the $y$ value increases.
- Negative correlation: as the $x$ value increases, the $y$ value decreases.
- No correlation: the $x$ and $y$ values do not have a relationship.
We can see from this graph that as the $x$ value increases, the $y$ value increases.
SolutionPositive correlation
As the $x$ value increases, the $y$ value increases.
-
Interpret the scatter graph.
HintsGo across the $x$ axis to $8$ and go directly up to the cluster of points. Estimate where you think the sales of hot chocolate would be if it fitted the pattern of the others.
Remember, this is an estimate so we are following an imaginary line through the middle of the points to get the best estimate we can.
When you go up to the points from $8$, move left from where you think the vertical line would hit a line going through the middle of the points. Take it across horizontally from there to the $y$ axis to read off the estimate for the amount of hot chocolates sold.
SolutionEstimated answer is $100$ to $120$ hot chocolates sold.
From the graph, we can see $100$ is a good estimate but it is slightly higher, so $100$ to $120$ seems fair.


 Do you want to learn faster and more easily?
Do you want to learn faster and more easily?






